题目内容
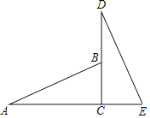
【题目】如图,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC 交 AC 于 D,CE 平分∠ACB 交 BD 于 E,图中 等腰三角形的个数是( )

A.3 个B.4 个C.5 个D.6 个
【答案】C
【解析】
在△ABC中,AB=AC,∠A=36°,可得∠ABC=∠ACB=72°,根据BD和CE是角平分线得出∠ABD=∠EBC=∠ACE=∠ECB=36°,再根据三角形的外角定理得出:∠CDE=∠CED=72°,再根据上面等腰三角形的判定定理判断即可.
∵AB=AC,∠A=36°
∴△ABC是等腰三角形,且∠ABC=∠ACB=![]()
又∵BD 平分∠ABC,CE 平分∠ACB
∴∠ABD=∠EBC=∠ACE=∠ECB=36°
∴△EBC是等腰三角形
∵∠ABD=∠A=36°
∴△ABD是等腰三角形
∵∠CED=∠ECB+∠EBC=72°且∠CDE=∠ABD+∠A=72°
∴∠CED=∠CDE=∠ACB=72°
∴△EDC和△BCD是等腰三角形
综上所述共有5个等腰三角形.
故选:C.

练习册系列答案
相关题目
【题目】为选派一名学生参加全市实践活动技能竞赛,A.B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如下图表所示(单位:mm)
平均数 | 方差 | 完全符合要求个数 | |
A | 20 | 0.026 | 2 |
B | 20 | SB2 |
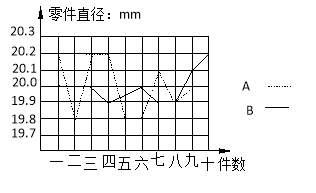
根据测试得到的有关数据,试解答下列问题:
⑴ 考虑平均数与完全符合要求的个数,你认为 的成绩好些;
⑵ 计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些;
⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由。