题目内容
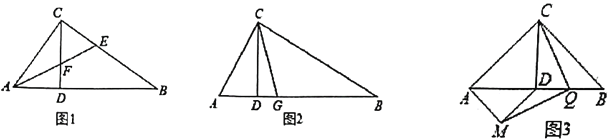
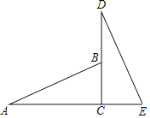
【题目】如图,已知C是线段AE上一点,
,
,B是CD上一点,CB=CE
1
求证：
≌
；
2若∠E=65°,求∠A的度数；
3若AE=11，BC=3，求BD的长,直接写出结果
【答案】（1）见解析；（2）∠A＝25°；（3）BD＝5.
【解析】
（1）由“SAS”可证△ACB≌△DCE；
（2）由全等三角形的性质和直角三角形的性质可得∠A的度数；
（3）根据题意可得AC＝DC，BC＝CE＝3，根据线段和差即可求BD的长．
解（1）∵DC＝AC，∠ACB＝∠DCE＝90°，BC＝CE，
∴△ACB≌△DCE（SAS）；
（2）∵△ACB≌△DCE，
∴∠E＝∠ABC＝65°，
∴∠A＝90°∠ABC＝25°；
（3）∵AC＝DC，BC＝CE＝3，
∴CD＝AC＝AECE＝113＝8，
∴BD＝CDBC＝83＝5.
练习册系列答案
阅读快车系列答案
相关题目
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表：
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分，求x和y的值；
(2)在(1)的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值．
