题目内容
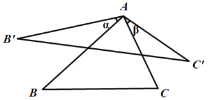
【题目】如图，将△ABC的边AB绕着点A顺时针旋转
（
）得到AB′，边AC绕着点A逆时针旋转
（
）得到AC′，联结B′C′,当+=60°时，我们称
AB′C′是ABC的“双旋三角形”，如果等边ABC的边长为a, 那么它所得的“双旋三角形”中B′C′=___________（用含a的代数式表示）.
【答案】
【解析】
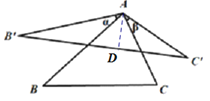
作AD⊥B′C′于点D，根据题意与旋转和等边三角形的的性质可得，△AB′C′是顶角为120°的等腰三角形，再根据等腰三角形的性质可得∠DA B′=60°，B′C′=2 B′D，根据sin∠DA B′=
即可得解.
解：作AD⊥B′C′于点D，
∵△ABC为等边三角形，
+
=60°，
∴AB′=AC′，∠B′AC′=120°，
∴∠B′=30°，∴B′D=
a，
则B′C′=.
故答案为：.
练习册系列答案
相关题目
