��Ŀ����
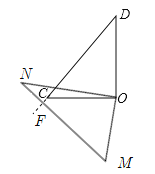
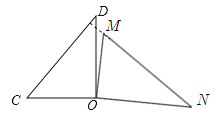
����Ŀ����ͼ�٣���һ��ֱ�����ǰ����ͬһ��ֱ��AB�ϣ����С�ONM��30�㣬��OCD��45�㣮

��1����ͼ���е����ǰ�OMN��BA�ķ���ƽ����ͼ�ڵ�λ�ã�MN��CD�ཻ�ڵ�E�����CEN�Ķ�����
��2����ͼ���е����ǰ�OMN�Ƶ�O����ʱ�뷽����ת��ʹ��BON��30�㣬��ͼ�ۣ�MN��CD�ཻ�ڵ�E�����CEN�Ķ�����
��3����ͼ���е����ǰ�OMN�Ƶ�O��ÿ��30����ٶȰ���ʱ�뷽����תһ�ܣ�����ת�Ĺ����У��ڵ�____________��ʱ��ֱ��MNǡ����ֱ��CD��ֱ����ֱ��д�������
���𰸡���1��105�㣻��2��135�㣻��3��5.5��11.5.
��������
��1���ڡ�CEN�У����������ڽǺͶ������������
��2���ɡ�BON��30������N=30���ɵ�MN��CB���ٸ�����ֱ��ƽ�У�ͬ���ڽǻ������������CEN�Ķ���.
��3������ͼ�Σ������MN��CDʱ����ת�ǣ��ٳ���30�����ý��.
�⣺��1���ڡ�CEN�У���CEN=180������ECN����CNE=180����45����30��=105����
��2���ߡ�BON��30������N=30����
���BON����N��
��MN��CB.
���OCD+��CEN=180����
�ߡ�OCD=45��
���CEN=180����45��=135����
��3����ͼ��MN��CDʱ����ת��Ϊ360����90����45����60��=165������360������60����45����=345���������ڵ�165���30��=5.5��345���30��=11.5��ʱ��ֱ��MNǡ����ֱ��CD��ֱ��