题目内容
【题目】如图,△ABC中,∠BAC=60°,
(1)如果△ABC角平分线BD、CE相交与点O,则∠BOC_________。
(2)如果△ABC的高BD、CE相交与点O,求∠BOC的度数。


【答案】(1)=120;(2)∠BOC =120°.
【解析】
(1)根据三角形内角和定理和角平分线定义求出∠OBC+∠OCB的度数,然后在△BOC中通过三角形内角和定理可求出∠BOC的度数;
(2)由高线的定义可知∠AEC=90°,∠ADB=90°,然后根据四边形内角和定理可求出∠DOE,问题得解.
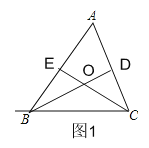
解(1)如图1,
∵∠BAC=60°,
∴∠ABC+∠ACB=180°-∠BAC=120°,
∵BD、CE分别是∠ABC,∠ACB的角平分线,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() ∠ABC+
∠ABC+![]() ∠ACB=
∠ACB=![]() (∠ACB+∠ACB)=60°,
(∠ACB+∠ACB)=60°,
∴∠BOC=180°-(∠OBC+∠OCB)=120°;
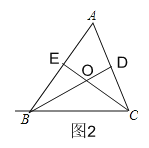
(2)如图2,
∵∠BAC=60°,BD、CE是△ABC的高线,
∴∠AEC=90°,∠ADB=90°,
∴∠DOE=360°-∠BAC-∠AEC-∠ADB=360°-60°-90°-90°=120°,
∴∠BOC=∠DOE=120°.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?






