Question

【题目】直线AB与直线CD相交于点O，OE平分.

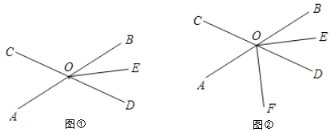
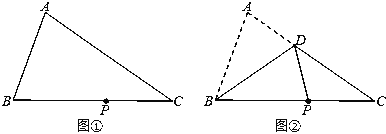
（1）如图①，若，求的度数；

（2）如图②，射线OF在内部.

①若，判断OF是否为的平分线，并说明理由；

②若OF平分，，求的度数.

Answer 1

【答案】（1）∠AOE=155°；（2）①DF平分∠AOD，证明见解析；②∠BOD=60°

【解析】

（1）由∠BOC=130°可得∠BOD=50°根据OE平分∠BOD得，根据对顶角相等可得∠AOD=∠BOC=130°即可求出∠AOE的度数；

（2）①由OE平分∠BOD可得∠BOE=∠DOE由OF⊥OE可得∠EOF=90°，故∠DOF=90°-∠DOE由图形可计算出：∠AOF=90°-∠BOE，故∠AOF=∠DOF可证DF平分∠AOD

②依题意设∠DOF=3x，则∠AOF=5x由OF平分∠AOE，可得∠EOF=∠AOF=5x，∠AOE=10x，可得：∠DOE=∠EOF-∠DOF=5x-3x=2x由OE平分∠BOD可得∠BOE=∠DOE=2x，∠BOD=4x由图形可知∠BOE+∠AOE=180°，列出方程求出x即可

(1) ∵∠BOC=130°

∴∠BOD=180°-∠BOC=180°-130°=50°

∵OE平分∠BOD

∴

∴∠AOD=∠BOC=130°

∴∠AOE=∠AOD+∠DOE=130°+25°=155°

(2) ①∵OE平分∠BOD

∴∠BOE=∠DOE

∵OF⊥OE

∴∠EOF=90°

∴∠DOF=90°-∠DOE

∵∠AOF=180°-∠EOF-∠BOE

=180°-90°-∠BOE

=90°-∠BOE

∴∠AOF=∠DOF

∴DF平分∠AOD

②∵

∴设∠DOF=3x，则∠AOF=5x

∵OF平分∠AOE

∴∠EOF=∠AOF=5x，∠AOE=10x

∴∠DOE=∠EOF-∠DOF=5x-3x=2x

∵OE平分∠BOD

∴∠BOE=∠DOE=2x，∠BOD=4x

∵∠BOE+∠AOE=180°

∴2x+10x=180°

∴x=15°

∴∠BOD=4×15°=60°