题目内容
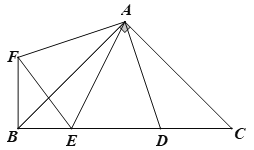
【题目】如图
、
，在平行四边形
中，
、
的角平分线
、
分别与线段
两侧的延长线（或线段）相交与
、
，与相交于点
.
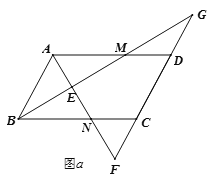
（1）在图中，求证：
，
.
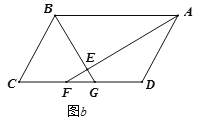
（2）在图中，仍有（1）中的，成立，请解答下面问题：
①若
，
，
，求
和的长；
②是否能给平行四边形的边和角各添加一个条件，使得点恰好落在边上且
为等腰三角形？若能，请写出所给条件；若不能，请说明理由.
【答案】（1）见解析；（2）①
，
，②
，
，见解析.
【解析】
（1）由平行线的性质和角平分线的性质即可证明结论；
（2）①由（1）题的思路可求得FG的长，再证明△BCG是等边三角形，从而得
，过点
作
交
延长线于点
，在Rt△AFH中用勾股定理即可求出AF的长；
②若使点
恰好落在边上且
为等腰三角形，易得F、G两点重合于点E，再结合（1）（2）的结论进行分析即可得到结论.
解：（1）∵四边形
是平行四边形，∴
，
.
∴
，
又∵
、
是
与
的角平分线，
∴
，即∠AEB=90°，
∴
，
∵
，∴
，
又∵是的角平分线、
∴
，
∴
.
同理可得
.
∴
；
（2）解：①由已知可得，、仍是与的角平分线且
，
，
，
，
.
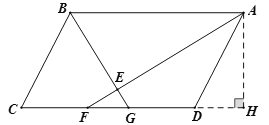
如图，过点作交延长线于点.
∵
，
，
.
.
∵
，
，
，
，
，
，
.
②，（类似答案均可）.
若使点恰好落在边上，则易得F、G两点重合于点E，又由（1）（2）的结论知，，所以平行四边形的边应满足；
若使点恰好落在边上且为等腰三角形，则EA=EB，所以∠EAB=∠EBA，
又因为、仍是与的角平分线，所以∠CBA=∠BAD=90°，所以∠C=90°.
练习册系列答案
阅读快车系列答案
相关题目
