题目内容
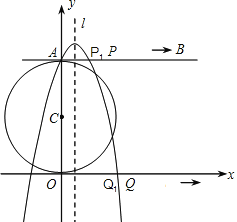
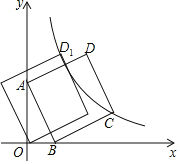
【题目】如图,直线AB与x的正半轴交于点B,且B(1,0),与y的正半轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=![]() (k≠0)上,将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y=![]() (k≠0)上的点D1处,则k=_____.
(k≠0)上的点D1处,则k=_____.
![]()
【答案】4
【解析】
设A(t,0),利用BA绕点B顺时针旋转90°得到BC,则可表示出C(t+1,1),利用正方形的性质,由于B点向右平移t个单位,向上平移1个单位得到C点,所以A点向右平移t个单位,向上平移1个单位得到D点,所以D(t,t+1),则D′(t-2,t+1),根据反比例函数图象上点的坐标特征得到k=t+1=(t-2)(t+1),然后先求出t,从而得到k的值.
解:设A(t,0),
∵四边形ABCD为正方形,
∴BA=BC,∠BAC=90°,
∴把BA绕点B顺时针旋转90°得到BC,
∴C(t+1,1),
∵B点向右平移t个单位,向上平移1个单位得到C点,
∴A点向右平移t个单位,向上平移1个单位得到D点,即D(t,t+1),
∵D点向左平移2个单位得到D′,
∴D′(t﹣2,t+1),
∵C(t+1,1),D′(t﹣2,t+1)在双曲线y=![]() (k≠0)上,
(k≠0)上,
∴k=t+1=(t﹣2)(t+1),
整理得t2﹣2t﹣3=0,解得t1=﹣1(舍去),t2=3,
∴t=3,
∴k=3+1=4.
故答案为4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目