Question

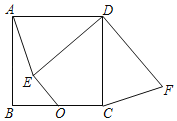
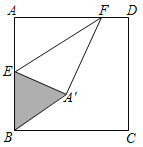
【题目】如图，四边形ABCD是边长为m的正方形，若AF＝m，E为AB上一点且BE＝3，把△AEF沿着EF折叠，得到△A'EF，若△BA'E为直角三角形，则m的值为_____．

Answer 1

【答案】12或

【解析】

分两种情况讨论：①当时，分别用含m的式子表示出，然后利用勾股定理即可求出m的值；②当时, 首先证明四边形是正方形，然后利用正方形的性质即可求解．

根据E为AB上一个动点，

把△AEF沿着EF折叠，得到，

若为直角三角形，

分两种情况讨论：

①当时，如图1，

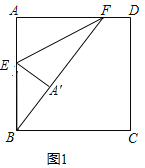
点B、A'、F三点共线，

根据翻折可知：

∵AF＝＝，AB＝m，

∴BF＝m，

∴，

∵BE＝3，

∴AE＝＝m﹣3，

∵，

∴，

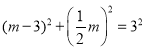解得，m＝，或m＝0（舍），

故m＝；

②当时，如图2，

∴，

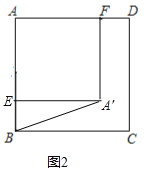
根据翻折可知：, AF＝＝

∴四边形是正方形，

∴EA＝m，

∴BE＝AB﹣AE＝m＝3，

∴m＝12，

综上，m＝12或，

故答案为：12或．