��Ŀ����
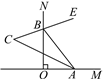
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У���A������Ϊ����2��2������B������Ϊ��6��6���������߾���A��O��B���㣬����OA��OB��AB���߶�AB��y���ڵ�E��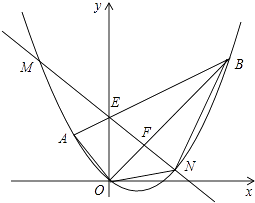
��1�����E�����ꣻ
��2���������ߵĺ�������ʽ��
��3����FΪ�߶�OB�ϵ�һ�����㣨�����O��B�غϣ���ֱ��EF�������߽���M��N���㣨��N��y���Ҳࣩ������ON��BN������F���߶�OB���˶�ʱ�����BON��������ֵ���������ʱ��N�����ꣻ
��4������AN������BON������ʱ��������ƽ������ʹ�á�BOP���OAN���ƣ���B��O��P�ֱ����O��A��N��Ӧ���ĵ�P�����꣮
���𰸡�
��1��
�⣺��ֱ��AB����ʽΪy=kx+b��
��A����2��2����B��6��6�����룬�� ![]() �����
����� ![]() ��
��
��y= ![]() x+3����x=0��
x+3����x=0��
��E��0��3��
��2��
�⣺�������߽���ʽΪy=ax2+bx+c��
��A����2��2����B��6��6����O��0��0������������룬��  �����
�����  ��
��
��y= ![]() x2��
x2�� ![]() x
x
��3��
�⣺�����⣬��ֱ��OB�Ľ���ʽΪy=x�����N������ֱ��OBƽ�е�ֱ�߽���ʽΪy=x+m��
����  ����x2��6x��4m=0������=36+16m=0ʱ����N����OBƽ�е�ֱ������������Ψһ�Ĺ����㣬���N��BO�ľ���������ԡ�BON������
����x2��6x��4m=0������=36+16m=0ʱ����N����OBƽ�е�ֱ������������Ψһ�Ĺ����㣬���N��BO�ľ���������ԡ�BON������
���m=�� ![]() ��x=3��y=
��x=3��y= ![]() ����N��3��
����N��3�� ![]() ����
����
��ʱ��BON���= ![]() ��6��6��
��6��6�� ![]() ��
�� ![]() +6����3��
+6����3�� ![]() ��
�� ![]() ��3=
��3= ![]()
��4��
�⣺����A��AS��GQ��S��

��A����2��2����B��6��6����N��3�� ![]() ����
����
�ߡ�AOE=��OAS=��BOH=45�㣬
OG=3��NG= ![]() ��NS=
��NS= ![]() ��AS=5��
��AS=5��
��Rt��SAN��Rt��NOG��
��tan��SAN=tan��NOG= ![]() ��
��
���SAN=��NOG��
���OAS����SAN=��BOG����NOG��
���OAN=��NOB��
��ON���ӳ����ϴ���һ��P��ʹ�á�BOP�ס�OAN��
��A����2��2����N��3�� ![]() ����
����
�ߡ�BOP���OAN���ƣ���B��O��P�ֱ����O��A��N��Ӧ��������BOP�ס�OAN��
��BO��OA=OP��AN=BP��ON
�֡�A����2��2����N��3�� ![]() ����B��6��6����
����B��6��6����
��BO=6 ![]() ��OA=2
��OA=2 ![]() ��AN=
��AN= ![]() ��ON=
��ON= ![]() ��
��
��OP= ![]() ��BP=
��BP= ![]() ��
��
��P��������4x��x����
��16x2+x2=�� ![]() ��2��
��2��
���x= ![]() ��4x=15��
��4x=15��
��P��P�����ֱ��y=x��Գƣ�
��P��������15�� ![]() ����
���� ![]() ��15����
��15����
����������1������A��B����������ֱ��AB�Ľ���ʽ����x=0������E�����ꣻ��2���������߽���ʽΪy=ax2+bx+c����A����2��2����B��6��6����O��0��0������������룬�з�������a��b��c��ֵ���ɣ���3�������⣬��ֱ��OB�Ľ���ʽΪy=x�����N������ֱ��OBƽ�е�ֱ�߽���ʽΪy=x+m���������߽���ʽ�������ó�����x��һԪ���η��̣�����=0ʱ����BON�������ɴ˿���m��ֵ��N������ꣻ��4���������������Ƶ����ʵõ�BO��OA=OP��AN=BP��ON��Ȼ����ݹ��ɶ����ֱ�����BO=6 ![]() ��OA=2
��OA=2 ![]() ��AN=
��AN= ![]() ��ON=
��ON= ![]() �����������OP=
�����������OP= ![]() ��BP=
��BP= ![]() ����P������Ϊ��x��y���������ù��ɶ����õ�����x��y�ķ����飬�ⷽ���鼴�ɣ�
����P������Ϊ��x��y���������ù��ɶ����õ�����x��y�ķ����飬�ⷽ���鼴�ɣ�