Question

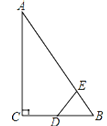
【题目】如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒，连接DE，当△BDE是直角三角形时，t的值______________．

Answer 1

【答案】2或3.5

【解析】∵∠ACB=90°,∠ABC=60°，BC=2cm，

∴AB=BC÷cos60°=2÷=4(cm)，

①∠BDE=90°时，

∵D为BC的中点，

∴DE是△ABC的中位线，

∴AE=AB=×4=2(cm)，

点E在AB上时,t=2÷1=2(秒)，

②∠BED=90°时,BE=BDcos60°=×2×=0.5(cm)

点E在AB上时,t=(40.5)÷1=3.5(秒)，

综上所述，t的值为2秒或3.5秒，

故答案为：2秒或3.5秒.

点睛: 本题主要考查锐角三角函数，用t表示出线段的长，化动为静，再根据60°角的三角函数值找到关于t的方程是解决这类问题的基本思路．