题目内容
【题目】已知等腰Rt△ABC,∠BAC=90°,AB=AC,点D为△ABC内部一点,连接AD、BD、CD,点H为BD中点,连接AH,且∠BAH=∠ACD.
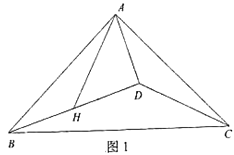
(1)如图1,若∠ADB=90°,求证:∠DAH=45°;
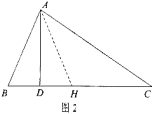
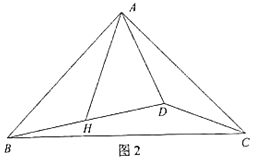
(2)如图2,若∠ADB<90°,(1)问中的结论是否成立,若成立,请证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)成立.
【解析】
(1)用ASA证明△ABH≌△CAD,得到BH=AD,即AD=HD,得到△AHD是等腰直角三角形,即可得出结论;
(2)延长AH到E,使HE=AH,连接DE.延长CD交AB于F,交AH于G.通过证明△ABH≌△EDH和△EGD≌△CGA,得到△AGD为等腰直角三角形,即可得出结论.
(1)∵∠BAC=90°,∴∠CAD+∠BAD=90°.
∵∠ADB=90°,∴∠ABH+∠BAD=90°,∴∠CAD=∠ABH.
在△ABH和△CAD中,∵∠BAH=∠ACD,AB=CA,∠ABH=∠CAD,∴△ABH≌△CAD(ASA),∴BH=AD.
∵H为BD的中点,∴BH=HD,∴AD=HD,∴△AHD是等腰直角三角形,∴∠DAH=45°.
(2)成立.理由如下:
如图,延长AH到E,使HE=AH,连接DE.延长CD交AB于F,交AH于G.
∵BH=DH,∠BHA=∠DHE,AH=EH,∴△ABH≌△EDH,∴AB=ED,∠1=∠E.
∵AB=AC,∴ED=AC.
∵∠1=∠2,∴∠E=∠2.
∵∠BAC=90°,∴∠1+∠GAC=90°.
∵∠1=∠2,∴∠2+∠GAC=90°,∴∠AGC=90°,∴∠EGD=∠CGA=90°.
在△EGD和△CGA中,∵∠E=∠2,∠EGD=∠CGA,ED=CA,∴△EGD≌△CGA(AAS),∴GD=GA,∴△AGD为等腰直角三角形,∴∠DAH=45°.

【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?