题目内容
【题目】如图,在半径为 ![]() 的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )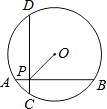
A.1
B.![]()
C.2
D.2 ![]()
【答案】B
【解析】解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,如图, 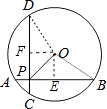
则AE=BE= ![]() AB=2,DF=CF=
AB=2,DF=CF= ![]() CD=2,
CD=2,
在Rt△OBE中,∵OB= ![]() ,BE=2,
,BE=2,
∴OE= ![]() =1,
=1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
而OE=OF=1,
∴四边形OEPF为正方形,
∴OP= ![]() OE=
OE= ![]() .
.
所以答案是:B.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】“2018年西安女子半程马拉松”的赛事有两项:A“女子半程马拉松”;B、“5公里女子健康跑”.小明对部分参赛选手作了如下调查:
调查总人数 | 50 | 100 | 200 | 300 | 400 | 500 |
参加“5公里女子健康跑”人数 | 18 | 45 | 79 | 120 | 160 | b |
参加“5公里女子健康跑”频率 | 0.360 | a | 0.395 | 0.400 | 0.400 | 0.400 |

(1)计算表中a,b的值;
(2)在图中,画出参赛选手参加“5公里女子健康跑“的频率的折线统计图;
(3)从参赛选手中任选一人,估计该参赛选手参加“5公里女子健康跑”的概率(精确到0.1).