题目内容
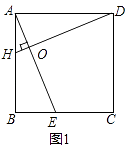
【题目】（10分）如图，△ABC中，边AB、AC的垂直平分线分别交BC于D、E．
（1）若BC=10，则△ADE周长是多少？为什么？
（2）若∠BAC=128°，则∠DAE的度数是多少？为什么？
【答案】（1）△ADE周长为10；（2）∠DAE=76°．
【解析】
试题（1）根据垂直平分线性质得AD=BD，AE=EC．所以△ADE周长=BC；
（2）∠DAE=∠BAC﹣（∠BAD+∠CAE）．根据三角形内角和定理及等腰三角形性质求解．
解：（1）C△ADE=10．
∵AB、AC的垂直平分线分别交BC于D、E，
∴AD=BD，AE=CE．
C△ADE=AD+DE+AE=BD+DE+CE=BC=10．
（2）∠DAE=76°．
∵AB、AC的垂直平分线分别交BC于D、E，
∴AD=BD，AE=CE．
∴∠B=∠BAD，∠C=∠CAE．
∵∠BAC=128°，
∴∠B+∠C=52°．
∴∠DAE=∠BAC﹣（∠BAD+∠CAE）
=∠BAC﹣（∠B+∠C）=76°．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】为庆祝“六一”儿童节，某市中小学统一组织文艺汇演，甲、乙两所学校共92人（其中甲校的人数多于乙校的人数，且甲校的人数不足90人）准备统一购买服装参加演出；下面是某服装厂给出的演出服装的价格表
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
（1）如果两所学校分别单独购买服装一共应付5000元，甲、乙两所学校各有多少学生准备参加演出？
（2）如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出，请你为两所学校设计一种最省钱的购买服装方案．
