题目内容
【题目】阅读下面材料:小明遇到这样一个问题:
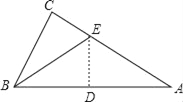
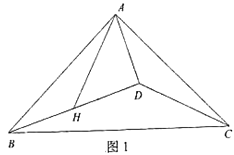
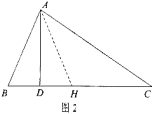
如图1,在△ABC中,∠B=2∠C,AD⊥BC于点D,求证:BC=AB+2BD.
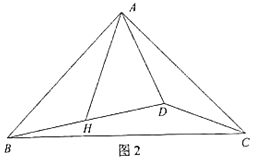
小明利用条件AD⊥BC,在CD上截取DH=BD,如图2,连接AH,既构造了等腰△ABH,又得到BH=2BD,从而命题得证。
(1)根据阅读材料,证明:BC=AB+2BD;
(2)参考小明的方法,解决下面的问题:
如图3,在△ABC中,∠BAC=90°,∠ABD=∠BCE,∠ABC=∠DCE,请探究AD与BE的数量关系,并说明理由。


【答案】(1)证明见解析;(2)BE=2AD.
【解析】
(1)由BD=DH,AD⊥BH,得到AB=AH,由等边对等角得到∠B=∠AHB,再由∠B=2∠C和三角形外角的性质得到∠C=∠CAH,由等角对等边得到AH=HC,即有AB=HC,从而可以得出结论;
(2)延长DA至点F,使得AF=AD,连接BF.设∠ABD=∠BCE=x,∠ABC=∠DCE=y.
证明BA垂直平分DF,得到BF=BD,∠1=∠DBA=x,进而得到∠FBC=∠ACB,由等角对等边得到BF=CF,即有BD=FC.由三角形外角的性质得到∠2=∠DCE,则有DE=DC,结合BD=CF,即可得到结论.
(1)∵BD=DH,AD⊥BH,∴AB=AH,∴∠B=∠AHB.
∵∠B=2∠C,∴∠AHB=2∠C=∠C+∠CAH,∴∠C=∠CAH,∴AH=HC,∴AB=HC,∴BC=HC+BH=AB+2BD.
(2)BE=2AD.理由如下:
延长DA至点F,使得AF=AD,连接BF.设∠ABD=∠BCE=x,∠ABC=∠DCE=y.
∵AF=AD,∠BAD=90°,∴BA垂直平分DF,∴BF=BD,∠1=∠DBA=x,∴∠FBC=∠1+∠ABC=x+y,∠ACB=∠DCE+∠ECB=x+y,∴∠FBC=∠ACB,∴BF=CF.
∵BF=BD,∴BD=FC.
∵∠2=∠3+x=∠ABC=y=∠DCE,∴DE=DC.
∵BD=FC,∴BE+DE=2AD+DC,∴BE=2AD.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】学期结束前,学校想调查七年级学生对新课改实验教材的意见,特向七年级480名学生作了问卷调查,结果如下表所示:
意见 | 非常喜欢 | 喜欢 | 有一点喜欢 | 不喜欢 |
人数 | 240 | 192 | 44 | 4 |
(1)计算出每一种意见的人数占调查总人数的百分比;
(2)请作出反映此调查结果的扇形统计图;
(3)从统计图中你能得出什么结论?说说你的理由.