Question

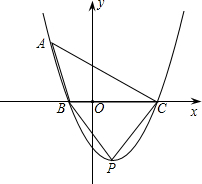
如图，直角坐标系中，O为坐标原点，A点坐标为（-3，0），B点坐标为（12，0），以AB为直径作⊙P与y轴的负半轴交于点C．抛物线y=ax²+bx+c经过A、B、C三点，其顶点为M点．
（1）求此抛物线的解析式；
（2）设点D是抛物线与⊙P的第四个交点（除A、B、C三点以外），求直线MD的解析式；
（3）判定（2）中的直线MD与⊙P的位置关系，并说明理由．

Answer 1

（1）连接PC，
∵A点坐标为（-3，0），B点坐标为（12，0），
∴AB=15，
∴AP=BP=PC=7.5，
∴OP=7.5-3=4.5，
∴OC=

PC2-OP2

=6，
∴C（0，-6）
把A（-3，0），B（12，0），C（0，6）代入y=ax²+bx+c得：

C=-6 0=9a-3b+c 0=144a+12b+c

，
解得：

a= 1 6 b=- 3 2 c=-6

，
∴y=

1

6

x²-

3

2

x-6；

（2）∵y=

1

6

x²-

3

2

x-6=

1

6

（x-

9

2

）x²-

75

8

；
∴M（

9

2

，-

75

8

），
∵P是圆的圆心，
∴PM是圆的对称轴，PM是抛物线的对称轴，
∵C（0，-6），
∴D（9，-6），
设直线MD的解析式y=kx+b，把D（9，-6）和M（

9

2

，-

75

8

）代入得：

-6=9k+b - 75 8 = 9 2 k+b

，
解得：

k= 3 4 b=- 51 4

，
∴y=

3

4

x-

51

4

；

（3）设直线DM和x轴交于E，连接PM，则PM⊥OE，过P作PD′⊥ME于D′，
设y=0，则y=

3

4

x-

51

4

=0，
∴x=17，
∴OE=17，∴E（17，0），
∴PE=17-4.5=12.5，
∵PM=

75

8

，
∴ME=

PE2+PM2

=

125

8

，
∵

1

2

PM•PE=

1

2

PD′•EM，
∴PD′=

15

2

=7.5，
∴PD′等于圆的半径，
∴直线MD与⊙P的位置关系是相切．