题目内容
唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望峰火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题--将军饮马问题:
如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河旁边的P点饮马后再到B点宿营.请问怎样走才能使总的路程最短?
作法如下:如(1)图,从B出发向河岸引垂线,垂足为D,在AP的延长线上,取B关于河岸的对称点B′,连接AB′,与河岸线相交于P,则P点就是饮马的地方,将军只要从A出发,沿直线走到P,饮马之后,再由P沿直线走到B,所走的路程就是最短的.
(1)观察发现
再如(2)图,在等腰梯形ABCD中,AB=CD=AD=2,∠D=120°,点E、F是底边AD与BC的中点,连接EF,在线段EF上找一点P,使BP+AP最短.
作点B关于EF的对称点,恰好与点C重合,连接AC交EF于一点,则这点就是所求的点P,故BP+AP的最小值为______.

(2)实践运用
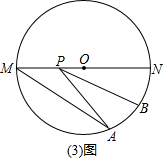
如(3)图,已知⊙O的直径MN=1,点A在圆上,且∠AMN的度数为30°,点B是弧AN的中点,点P在直径MN上运动,求BP+AP的最小值.
(3)拓展迁移
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
①求这条抛物线所对应的函数关系式;
②在抛物线的对称轴直线x=1上找到一点M,使△ACM周长最小,请求出此时点M的坐标与△ACM周长最小值.(结果保留根号)

如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河旁边的P点饮马后再到B点宿营.请问怎样走才能使总的路程最短?
作法如下:如(1)图,从B出发向河岸引垂线,垂足为D,在AP的延长线上,取B关于河岸的对称点B′,连接AB′,与河岸线相交于P,则P点就是饮马的地方,将军只要从A出发,沿直线走到P,饮马之后,再由P沿直线走到B,所走的路程就是最短的.
(1)观察发现
再如(2)图,在等腰梯形ABCD中,AB=CD=AD=2,∠D=120°,点E、F是底边AD与BC的中点,连接EF,在线段EF上找一点P,使BP+AP最短.
作点B关于EF的对称点,恰好与点C重合,连接AC交EF于一点,则这点就是所求的点P,故BP+AP的最小值为______.

(2)实践运用
如(3)图,已知⊙O的直径MN=1,点A在圆上,且∠AMN的度数为30°,点B是弧AN的中点,点P在直径MN上运动,求BP+AP的最小值.

(3)拓展迁移
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
①求这条抛物线所对应的函数关系式;
②在抛物线的对称轴直线x=1上找到一点M,使△ACM周长最小,请求出此时点M的坐标与△ACM周长最小值.(结果保留根号)

(1)∵在等腰梯形ABCD中,AB=CD=AD=2,∠D=120°,点E、F是底边AD与BC的中点,
∴∠DAC=∠DCA=30°,
∴∠ACB=30°,
∴∠BAC=90°,
∴tan∠ACB=
,
∴AC=
=2
,
故答案为:2
;
(2)如图,作点A关于MN的对称点A′,则A′在⊙O上,
连接BA′交MN于P′点,此时BP′+AP′最小.
由对称性可知AP′=A′P′,
∴BP′+AP′=BP′+A′P′=A′B,
连接OA、OB、OA′,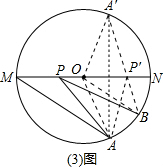
可知弧AN=弧A′N,
则∠NOA′=∠NOA=2∠M=60°,
而点B为弧AN中点,
∴∠BON=30°
∴∠BOA′=90°
而MN=1,
∴在Rt△OA′B中,A′B=
即BP+AP的最小值
.
(3)①∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、
C(0,-3)两点,分别代入二次函数解析式得: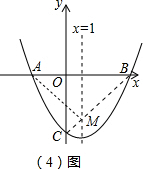
∴
,
解得:a=1,b=-2,c=-3,
∴二次函数解析式为:y=x2-2x-3,
②得到直线BC:y=x-3,
∴M(1,-2),AC的长为:
,
∴△ACM周长最小值即是:AM+CM最小时的值,
∵AM+CM=BC=3
,
∴△ACM周长最小值为:
+3
.
∴∠DAC=∠DCA=30°,
∴∠ACB=30°,
∴∠BAC=90°,
∴tan∠ACB=
| AB |
| AC |
∴AC=
| 2 | ||||
|
| 3 |
故答案为:2
| 3 |
(2)如图,作点A关于MN的对称点A′,则A′在⊙O上,
连接BA′交MN于P′点,此时BP′+AP′最小.
由对称性可知AP′=A′P′,
∴BP′+AP′=BP′+A′P′=A′B,
连接OA、OB、OA′,

可知弧AN=弧A′N,
则∠NOA′=∠NOA=2∠M=60°,
而点B为弧AN中点,
∴∠BON=30°
∴∠BOA′=90°
而MN=1,
∴在Rt△OA′B中,A′B=
| ||
| 2 |
即BP+AP的最小值
| ||
| 2 |
(3)①∵抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、
C(0,-3)两点,分别代入二次函数解析式得:

∴
|
解得:a=1,b=-2,c=-3,
∴二次函数解析式为:y=x2-2x-3,
②得到直线BC:y=x-3,
∴M(1,-2),AC的长为:
| 10 |
∴△ACM周长最小值即是:AM+CM最小时的值,
∵AM+CM=BC=3
| 2 |
∴△ACM周长最小值为:
| 10 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为直径作⊙D,设⊙D的半径为2.
为直径作⊙D,设⊙D的半径为2.
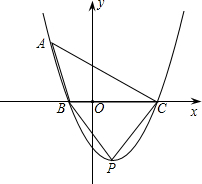

 半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.
半轴上.关于y轴对称的抛物线y=ax2+bx+c经过A、D(3,-2)、P三点,且点P关于直线AC的对称点在x轴上.

