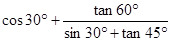题目内容
某校学生去春游,在风景区看到一棵汉柏树,不知这棵汉柏树有多高,下面是两位同学的一段对话:
小明:我站在此处看树顶仰角为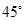 。
。
小华:我站在此处看树顶仰角为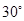 。
。
小明:我们的身高都是1.6m.
小华:我们相距20m。
请你根据这两位同学的对话,计算这棵汉柏树的高度。
(参考数据: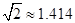 ,
,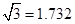 ,结果保留三个有效数字)
,结果保留三个有效数字)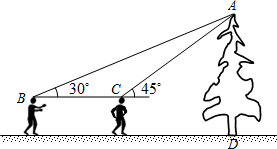
小明:我站在此处看树顶仰角为
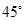 。
。小华:我站在此处看树顶仰角为
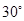 。
。小明:我们的身高都是1.6m.
小华:我们相距20m。
请你根据这两位同学的对话,计算这棵汉柏树的高度。
(参考数据:
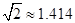 ,
,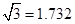 ,结果保留三个有效数字)
,结果保留三个有效数字)
28.9米
解:如图所示,延长BC交DA于E。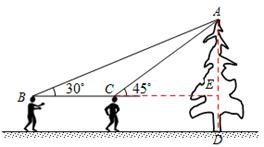
设AE的长为x m,
在Rt△ACE中,∠ACE=45°,∠AEB=90°,
∴∠CAE=45°, AE=CE=x。
在Rt△ABE中,∠B=30°,AE=x,
∴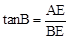 ,即:
,即: 。
。
∵BE-CE=BC,BC=20, ∴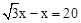 ,解得x=10
,解得x=10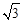 +10。
+10。
∴AD=AE+DE=10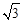 +10+1.6≈28.9(m)。
+10+1.6≈28.9(m)。
答:这棵汉柏树的高度约为28.9米。
延长BC交DA于E.设AE的长为x米,在Rt△ACE中,求得CE=AE,然后在Rt△ABE中求得BE,利用BE-CE=BC,解得AE,则AD=AE+DE。

设AE的长为x m,
在Rt△ACE中,∠ACE=45°,∠AEB=90°,
∴∠CAE=45°, AE=CE=x。
在Rt△ABE中,∠B=30°,AE=x,
∴
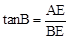 ,即:
,即: 。
。∵BE-CE=BC,BC=20, ∴
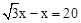 ,解得x=10
,解得x=10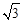 +10。
+10。∴AD=AE+DE=10
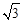 +10+1.6≈28.9(m)。
+10+1.6≈28.9(m)。答:这棵汉柏树的高度约为28.9米。
延长BC交DA于E.设AE的长为x米,在Rt△ACE中,求得CE=AE,然后在Rt△ABE中求得BE,利用BE-CE=BC,解得AE,则AD=AE+DE。

练习册系列答案
相关题目
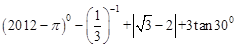 .
.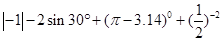
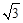 ≈1.73,精确到个位)
≈1.73,精确到个位)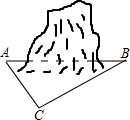
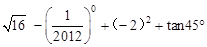 .
. 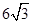 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
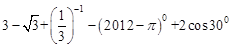 .
.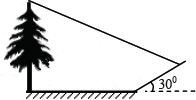
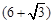 米
米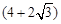 米
米