题目内容
如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为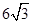 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
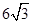 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
6.4米
解:∵底部B点到山脚C点的距离BC为6 3 米,山坡的坡角为30°.
∴DC=BC•cos30°=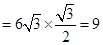 米,
米,
∵CF=1米,
∴DC=9+1=10米,
∴GE=10米,
∵∠AEG=45°,
∴AG=EG=10米,
在直角三角形BGF中,
BG=GF•tan20°=10×0.36=3.6米,
∴AB=AG-BG=10-3.6=6.4米,
答:树高约为6.4米
首先在直角三角形BDC中求得DC的长,然后求得DF的长,进而求得GF的长,然后在直角三角形BGF中即可求得BG的长,从而求得树高
∴DC=BC•cos30°=
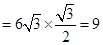 米,
米,∵CF=1米,
∴DC=9+1=10米,
∴GE=10米,
∵∠AEG=45°,
∴AG=EG=10米,
在直角三角形BGF中,
BG=GF•tan20°=10×0.36=3.6米,
∴AB=AG-BG=10-3.6=6.4米,
答:树高约为6.4米
首先在直角三角形BDC中求得DC的长,然后求得DF的长,进而求得GF的长,然后在直角三角形BGF中即可求得BG的长,从而求得树高

练习册系列答案
相关题目
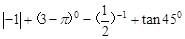
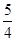
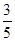
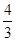
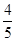
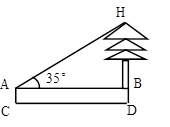
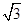 ,求树高AB。(结果保留整数,参考数据:
,求树高AB。(结果保留整数,参考数据: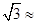 1.7)
1.7)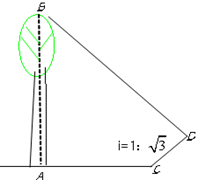
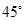 。
。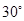 。
。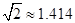 ,
,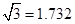 ,结果保留三个有效数字)
,结果保留三个有效数字)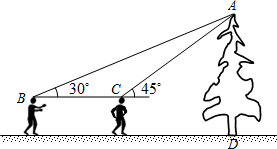
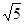

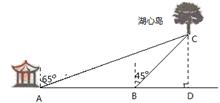
 处测得湖心岛上的迎宾槐
处测得湖心岛上的迎宾槐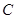 处位于北偏东
处位于北偏东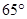 方向,然后,他从凉亭
方向,然后,他从凉亭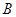 处,测得湖心岛上的迎宾槐
处,测得湖心岛上的迎宾槐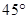 方向(点
方向(点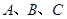 在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐
在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐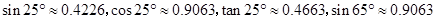 ,
,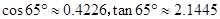 )
)