题目内容
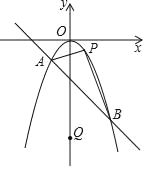
【题目】如图,已知抛物线![]() 分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
分别交x轴、y轴于点A(2,0)、B(0,4),点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若![]() .
.
①求抛物线的解析式;
②当线段PD的长度最大时,求点P的坐标;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与△AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.

【答案】(1) ①y=-2x2+2x+4;②P的坐标是(1,2); (2)见解析.
【解析】
(1)①把A、B的坐标代入抛物线解析式,由a+b=0,解方程组即可得出结论;
②设直线AB的解析式为![]() ,把A的坐标代入即可求出k的值,从而得到直线AB的解析式.设P点坐标为(m,﹣2m+4),则D(m,-2m2+2m+4),可表示出PD的长,利用二次函数的性质即可得出结论;
,把A的坐标代入即可求出k的值,从而得到直线AB的解析式.设P点坐标为(m,﹣2m+4),则D(m,-2m2+2m+4),可表示出PD的长,利用二次函数的性质即可得出结论;
(2)如图2,利用勾股定理计算出AB的长,再求出P的坐标,则可计算出PB的长,接着表示出抛物线解析式为y=ax2﹣2(a+1)x+4,则可用a表示出点D坐标为(1,2﹣a),所以PD=﹣a,由于∠DPB=∠OBA,根据相似三角形的判定方法,当![]() 时,△PDB∽△BOA,即
时,△PDB∽△BOA,即![]() ;当
;当![]() 时,△PDB∽△BAO,即
时,△PDB∽△BAO,即![]() ,然后解方程分别求出a的值,从而得到对应的抛物线的解析式.
,然后解方程分别求出a的值,从而得到对应的抛物线的解析式.
(1)①把A(2,0)、B(0,4)代入![]() 得:
得:![]() .
.
∵a+b=0,∴
∴![]() ,∴抛物线的解析式为y=-2x2+2x+4;
,∴抛物线的解析式为y=-2x2+2x+4;
②设直线AB的解析式为![]() ,则
,则![]() ,∴
,∴![]() ,∴直线AB的解析式为
,∴直线AB的解析式为![]() .
.
设P点坐标为(m,﹣2m+4),则D(m,-2m2+2m+4),∴PD=﹣2m2+2m+4﹣(﹣2m+4)=﹣2m2+4m![]() ,∴当
,∴当![]() 时,线段PD的长度最大,此时点P的坐标是(1,2).
时,线段PD的长度最大,此时点P的坐标是(1,2).
(2)存在.
如图2,OB=4,OA=2,则AB=![]() =2
=2![]() .
.
当x=1时,y=﹣2x+4=2,则P(1,2),∴PB=![]() =
=![]() .
.
把A(2,0)代入y=ax2+bx+4得4a+2b+4=0,解得:b=-2a-2,∴抛物线的解析式为y=ax2-2(a+1)x+4.
当x=1时,y=ax2-2(a+1)x+4=a-2a-2+4=2-a,则D(1,2-a),∴PD=2-a-2=﹣a.
∵DC∥OB,∴∠DPB=∠OBA.
当![]() 时,△PDB∽△BOA,即
时,△PDB∽△BOA,即![]() ,解得:a=-2,此时抛物线解析式为y=-2x2+2x+4;
,解得:a=-2,此时抛物线解析式为y=-2x2+2x+4;
当![]() 时,△PDB∽△BAO,即
时,△PDB∽△BAO,即![]() ,解得:a=-
,解得:a=-![]() ,此时抛物线解析式为y=-
,此时抛物线解析式为y=-![]() x2+3x+4.
x2+3x+4.
综上所述:满足条件的抛物线的解析式为y=﹣2x2+2x+4或y=-![]() x2+3x+4.
x2+3x+4.

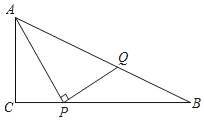
【题目】如图,Rt△ABC中,∠C=90°,P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q.已知AC=3cm,BC=6cm,设PC的长度为xcm,BQ的长度为ycm.
小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x,y),画出该函数的图象;
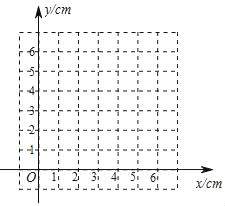
(3)结合画出的函数图象,解决问题:
①当y>2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?