Question

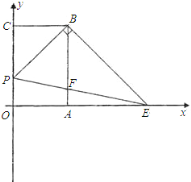
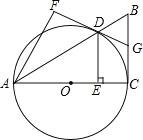
【题目】如图，已知Rt△ABC中，∠ACB=90°，以AC为直径的圆O交斜边AB于D．过D作DE⊥AC于E，将△ADE沿直线AB翻折得到△ADF．

（1）求证：DF是⊙O的切线；

（2）若⊙O的半径为10，sin∠FAD=，延长FD交BC于G，求BG的长．

Answer 1

【答案】（1）见解析（2）

【解析】

（1）由△ADE沿直线AB翻折得到△ADF，得到∠DAE=∠DAF，∠AED=∠F=90°，由于OA=OD，于是得到∠DAE=∠ODA，根据平行线的判定定理得到OD∥AF，根据平行线的性质得到OD⊥DF，于是得到结论；
（2）连接DC，由于AC是 O的直径，即CD⊥AB；又FD与BC均是 O的切线且相交于点G由切线长定理可得：GD=GC，于是得到∠GDC=∠GCD，由于GD是Rt△BDC斜边上的中线，即GD=BC，由于△ADE沿直线AB翻折得到△ADF，得到sin∠DAE=sin∠DAF=，解直角三角形得到sin∠DAC===，得DC=6，由勾股定理得AD=8；根据三角形相似即可得到结论．

(1)证明：

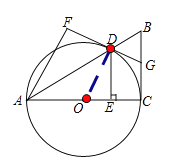
∵△ADE沿直线AB翻折得到△ADF，

∴∠DAE=∠DAF,∠AED=∠F=90°，

又∵OA=OD，

∴∠DAE=∠ODA，

∴∠DAF=∠ODA，

∴OD∥AF，

∴∠ODF+∠F=180°，

∴∠ODF=90°，

∴OD⊥DF，

∴DF是O的切线；

(2)连接DC,

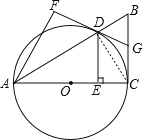
∵AC是圆O的直径，

∴∠ADC=90°，即CD⊥AB；

又∵FD与BC均是圆O的切线且相交于点G，

由切线长定理可得：GD=GC，

∴∠GDC=∠GCD，

又∵Rt△BDC中,∠GCD+∠B=90°,∠GDC+∠GDB=90°，

∴∠B=∠GDB，

∴GD=GB，

∴GD是Rt△BDC斜边上的中线,即GD=BC，

∵△ADE沿直线AB翻折得到△ADF，

∴∠DAE=∠DAF，

∴sin∠DAE=sin∠DAF=，

又∵圆O的半径为5，

∴AC=10，

Rt△DAC中,∠ADC=90°，

∴sin∠DAC=DCAC=DC10=，得DC=6，

由勾股定理得AD=8；

在Rt△ADC与Rt△ACB中,∠ADC=∠ACB=90°，∠DAC=∠BAC，

∴Rt△ADC∽Rt△ACB，

∴,即,解得BC=；

∴GB=GD=BC=.