题目内容
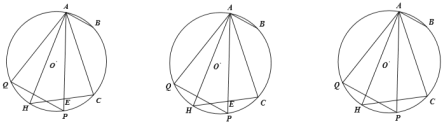
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ=2,将三角板CPQ绕点C旋转(点P在△ABC内部),连接AP、BP、BQ.

(1)求证:AP=BQ;
(2)当PQ⊥BQ时,求AP的长.
【答案】(1)见解析;(2)![]() ﹣
﹣![]()
【解析】
(1)欲证明PA=BQ,只要证明△ACP≌△BCQ即可;
(2)如图2中,作CH⊥PQ于H.首先证明A、P、Q共线,利用勾股定理求出AH,PH即可解决问题.
(1)证明:如图1中,
∵CA=CB,CP=CQ,∠ACB=∠PCQ=90°,
∴∠ACP=∠BCQ,
∴△ACP≌△BCQ,
∴PA=BQ.

(2)解:如图2中,作CH⊥PQ于H.
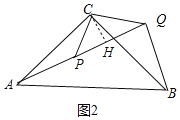
∵PQ⊥BQ,
∴∠PQB=90°,
∵∠CQP=∠CPQ=45°,
∴∠CQB=135°,
∵△ACP≌△CBQ,
∴∠APC=∠CQB=135°,
∴∠APC+∠CPQ=180°,
∴A、P、Q共线,
∵PC=2,
∴CH=PH=![]() ,
,
在Rt△ACH中,AH=![]() =
=![]() =
=![]() ,
,
∴PA=AH﹣PH=![]() ﹣
﹣![]() .
.

练习册系列答案
相关题目