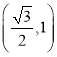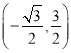题目内容
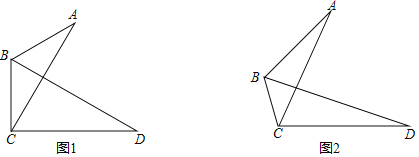
【题目】一个斜边长是8的Rt△AEC,一个斜边长是6的Rt△AFB,一个正方形AEDF,拼成一个如图所示的Rt△BCD,则Rt△AEC和Rt△AFB的面积之和是_____.

【答案】24
【解析】
设正方形AEDF的边长为x,则AE=AF=x,证明△AEC∽△BFA,利用相似比得到BF=![]() x,CE=
x,CE=![]() x,在Rt△ACE中利用勾股定理得到x2+(
x,在Rt△ACE中利用勾股定理得到x2+(![]() x)2=82,则x2=
x)2=82,则x2=![]() ,然后根据三角形面积公式计算Rt△AEC和Rt△AFB的面积之和.
,然后根据三角形面积公式计算Rt△AEC和Rt△AFB的面积之和.
设正方形AEDF的边长为x,则AE=AF=x,
∵AE∥BD,
∴∠CAE=∠B,
而∠AEC=∠AFB=90°,
∴△AEC∽△BFA,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴BF=![]() x,CE=
x,CE=![]() x,
x,
在Rt△ACE中,x2+(![]() x)2=82,
x)2=82,
∴x2=![]() ,
,
∴Rt△AEC和Rt△AFB的面积之和=![]() x
x![]() x+
x+![]() x
x![]() x=
x=![]() x2=
x2=![]() ×
×![]() =24.
=24.
故答案为24.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目