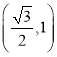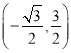��Ŀ����
����Ŀ����ѧ���ϣ���ʦ��ʾ�����¿��е���Ŀ��

С����ͬ��С�����ۺ��������½��
��1�����������̽������
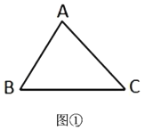
����EΪAB���е�ʱ����ͼ1��ȷ���߶�AE��DB�Ĵ�С��ϵ������ֱ��д�����ۣ�AE_______DB�����������������������
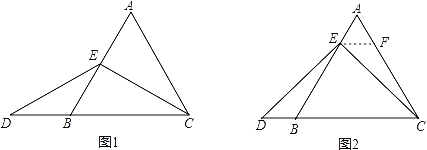
��2�����������������Ŀ
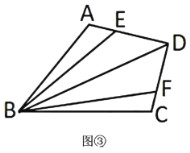
�⣺��Ŀ�У�AE��DB�Ĵ�С��ϵ�ǣ�AE�� ��DB����������������������������£���ͼ2������E��EF��BC����AC�ڵ�F����������ż���������½����̣�
��3����չ���ۣ��������
�ڵȱ�������ABC�У���E��ֱ����AB�ϣ���D��ֱ��BC�ϣ���ED��EC������ABC�ı߳�Ϊ3��AE��5����CD�ij�������ֱ��д���������
���𰸡���1��������2����������������3��CD�ij���8��2
��������
��1�����õ������������ߺ�һ�������Լ��ȱ������ε����ʿ��Եó���BCE=��ACE=30�㣬�ָ���ED=EC�õ���D=��ECD=30�㣬�ɽ�һ���ó���D=��DEB���Ƴ�BD=BE���ɽ�����⣻
��2����EF��BC��AC��F����֤����AEFΪ�ȱ������Σ���֤����DBE�ա�EFC���ɽ�����⣻
��3�����������Σ��ٵ���E��AB���ӳ����ϣ���D��CB���ӳ�����ʱ���ɣ�2��ͬ���ɵ�BD=AE���ٸ���CD=BD+BC�������������ڵ���E��BA���ӳ����ϣ���D��BC���ӳ�����ʱ����A��AN��BC��N����E��EM��CD��M�������CM�ij����Ӷ��ɵó�CD�ij����۵���E��AB���ӳ����ϣ���D��BC���ӳ�����ʱ�����ڡ�ECD����EBC����ʱ������EC��ED���ܵ���E��BA���ӳ����ϣ���D��CB���ӳ�����ʱ���С�ECD����EDC����ʱ��������ڣ�
�⣺��1����ͼ1�У����ۣ�AE=BD��
�ߡ�ABC�ǵȱ������Σ�AE=EB��
���BCE=��ACE=30�㣬��ABC=60�㣬
��ED=EC��
���D=��ECD=30�㣬
�ߡ�EBC=��D+��BED��
���D=��BED=30�㣬
��BD=BE=AE��
�ʴ�Ϊ��=��
��2��AE��DB��
�������£���ͼ2������E��EF��BC����AC�ڵ�F��
�ڵȱߡ�ABC�У���ABC����ACB����BAC��60����AB��BC��AC��
��EF��BC��
���AEF����ABC����AFE����ACB��
���AEF����AFE����BAC��60����
��AE��AF��EF��
��AB��AE��AC��AF��
��BE��CF��
�ߡ�ABC����EDB+��BED����ACB����ECB+��FCE��
��ED��EC��
���EDB����ECB��
���BED����FCE��
�ڡ�DBE�͡�EFC��
 ��
��
���DBE�ա�EFC��SAS����
��DB��EF��
��AE��BD��
�ʴ�Ϊ������
��3�������������
�ٵ���E��AB���ӳ����ϣ���D��CB���ӳ�����ʱ����ͼ��
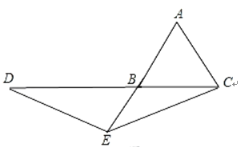
��AB��AC��3��AE��5��
ͬ��2���ɵ�BD=AE��
��BD��AE��5��
��CD��3+5��8��
�ڵ���E��BA���ӳ����ϣ���D��BC���ӳ�����ʱ����ͼ����A��AN��BC��N����E��EM��CD��M��
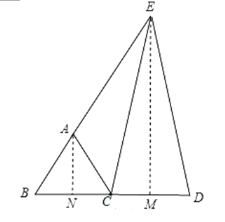
�ߵȱ�������ABC��
���AEM=90��-��B=30�㣬
��BM��![]() BE��
BE��![]() ����3+5����4��
����3+5����4��
��CM��BM-BC��4��3��1��
��EC=ED��EM��CD��
��CD��2CM��2��
�۵���E��AB���ӳ����ϣ���D��BC���ӳ�����ʱ����ͼ��
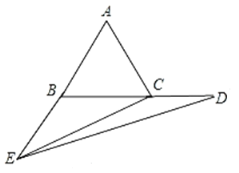
�ߡ�ECD����EBC����EBC��120����������ECD���ܴ���120���������EDC�������������ڽǺͶ�����
���ʱ������EC��ED��
�ܵ���E��BA���ӳ����ϣ���D��CB���ӳ�����ʱ����ͼ��
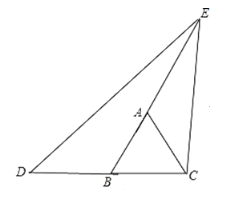
�ߡ�EDC����ABC����ECB����ACB��
�֡ߡ�ABC����ACB��60����
���ECD����EDC��
����ʱED��EC��
���ʱ��������ڣ�
����������CD�ij���8��2��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�