题目内容
【题目】如图①,将抛物线y=ax2(﹣1<a<0)平移到顶点恰好落在直线y=x﹣3上,并设此时抛物线顶点的横坐标为m.
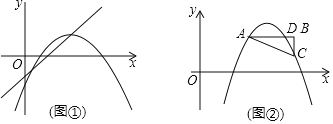
(1)求抛物线的解析式(用含a、m的代数式表示)
(2)如图②,Rt△ABC与抛物线交于A、D、C三点,∠B=90°,AB∥x轴,AD=2,BD:BC=1:2.
①求△ADC的面积(用含a的代数式表示)
②若△ADC的面积为1,当2m﹣1≤x≤2m+1时,y的最大值为﹣3,求m的值.
【答案】(1)y=ax2﹣2amx+am2+m﹣3;(2)①﹣![]() ;②0或
;②0或![]()
【解析】
(1)抛物线的顶点在直线y=x﹣3上,横坐标为m,则顶点的坐标为(m,m﹣3),即可求解;
(2)①求出点C坐标(m+1+t,a+m﹣3﹣2t),利用点C在抛物线上,则:a+m﹣3﹣2t=a(m+t+1﹣m)2+m﹣3,求得:t=﹣![]() ,利用S△ADC=
,利用S△ADC=![]() ADCB即可求解;②分m>2m+1、2m﹣1≤m≤2m+1、m<2m+1三种情况,求解即可.
ADCB即可求解;②分m>2m+1、2m﹣1≤m≤2m+1、m<2m+1三种情况,求解即可.
解:(1)抛物线的顶点在直线y=x﹣3上,横坐标为m,
则顶点的坐标为(m,m﹣3),
则抛物线的表达式为:y=a(x﹣m)2+m﹣3=ax2﹣2amx+am2+m﹣3;
(2)①如图所示,AB∥x轴,AD=2,
∴点D(m+1,a+m﹣3),
设:BD=t,
∵BD:BC=1:2,则BC=2t,
则点C(m+1+t,a+m﹣3﹣2t),
又点C在抛物线上,
则:a+m﹣3﹣2t=a(m+t+1﹣m)2+m﹣3,
解得:t=0(舍去)或﹣![]() ,
,
∴S△ADC=![]() ADCB=﹣
ADCB=﹣![]() ;
;
②若△ADC的面积为1,则=﹣![]() =1,
=1,
解得:a=﹣![]() ;
;
∴抛物线的表达式为:y=﹣![]() (x﹣m)2+m﹣3;
(x﹣m)2+m﹣3;
当m>2m+1时,即:m<﹣1时,
﹣![]() (2m+1﹣m)2+m﹣3=﹣3,
(2m+1﹣m)2+m﹣3=﹣3,
整理得:4m2+3m+4=0,
△=b
当2m﹣1≤m≤2m+1时,即:﹣1≤m≤1,
则m﹣3=﹣3,解得:m=0;
当m<2m﹣1时,即:m>1,
﹣![]() (2m﹣1﹣m)2+m﹣3=﹣3,
(2m﹣1﹣m)2+m﹣3=﹣3,
整理并解得:m=![]() (舍去负值),
(舍去负值),
故:m的值为:0或![]() .
.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案