题目内容
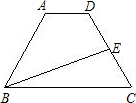
在等腰梯形ABCD中,AD∥BC,AD=3,BC=7,AB=CD,E为CD的中点,四边形ABED的周长与△BCE的周长之差为2,则AB的长为( )
| A.8 | B.3 | C.6 | D.7 |
如图所示,四边形ABCD的周长=AB+BE+DE+AD,△BCE的周长=BC+EC+BE,
∵四边形ABED的周长与△BCE的周长之差为2,
∴AB+BE+DE+AD-(BC+EC+BE)=AB+AD-BC=AB+3-7=2,
∴AB=6.
故选C.
∵四边形ABED的周长与△BCE的周长之差为2,
∴AB+BE+DE+AD-(BC+EC+BE)=AB+AD-BC=AB+3-7=2,
∴AB=6.
故选C.


练习册系列答案
相关题目