题目内容
如图在梯形ABCD中，AB=DC=10cm，AC与BD相交于G，且∠AGD=60°，设E为CG的中点，F为AB的中点，则EF的长为______cm．
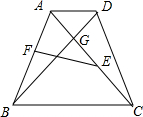
连接BE，
∵梯形ABCD中，AB=DC，
∴AC=BD，可证△ABC≌△DCB
∴∠GCB=∠GBC，
又∵∠BGC=∠AGD=60°
∴△BCG为等边三角形，
∵BE为△BCG的中线，
∴BE⊥AC，
在Rt△ABE中，EF为斜边AB上的中线，
∴EF=
AB=5cm．
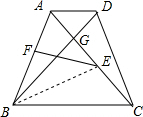
∵梯形ABCD中，AB=DC，
∴AC=BD，可证△ABC≌△DCB
∴∠GCB=∠GBC，
又∵∠BGC=∠AGD=60°
∴△BCG为等边三角形，
∵BE为△BCG的中线，
∴BE⊥AC，
在Rt△ABE中，EF为斜边AB上的中线，
∴EF=
| 1 |
| 2 |
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
