题目内容
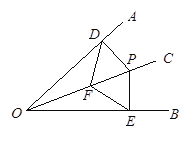
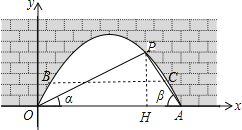
【题目】图中是抛物线拱桥,P处有一照明灯,点P到水面OA的距离为![]() ,从O、A两处观测P处,仰角分别为
,从O、A两处观测P处,仰角分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为
,以O为原点,OA所在直线为x轴建立直角坐标系,已知抛物线方程为![]() .
.
![]() 求抛物线方程,并求抛物线上的最高点到水面的距离;
求抛物线方程,并求抛物线上的最高点到水面的距离;
![]() 水面上升1m,水面宽多少
水面上升1m,水面宽多少![]() 取
取![]() ,结果精确到
,结果精确到![]() ?
?
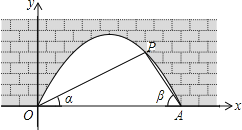
【答案】(1)故抛物线方程为![]() ,抛物线上的最高点到水面的距离2m;
,抛物线上的最高点到水面的距离2m;
(2)水面宽约为![]() .
.
【解析】
(1)如图过点P作![]() 于H,求出
于H,求出![]() 中OH的长得到P点坐标,再求出
中OH的长得到P点坐标,再求出![]() 中AH长得到A点坐标为(4,0),所以可设抛物线解析式为
中AH长得到A点坐标为(4,0),所以可设抛物线解析式为![]() ,然后将P点坐标代入求解得到抛物线解析式,然后求出顶点坐标即可得到答案;
,然后将P点坐标代入求解得到抛物线解析式,然后求出顶点坐标即可得到答案;
(2)将y=1代入抛物线解析式中求解得到x的值,然后计算出水面宽即可.
(1)过点P作![]() 于H,如图.
于H,如图.
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() ,
,
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∴点A坐标为(4,0),
过点![]() ,
,![]() 的抛物线的解析式可设为
的抛物线的解析式可设为![]() ,
,
![]() 在抛物线
在抛物线![]() 上,
上,
![]() ,
,
解得![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() =
=![]() ,
,
∴抛物线的顶点坐标为(2,2),
则抛物线上的最高点到水面的距离2m,
故抛物线方程为![]() ,抛物线上的最高点到水面的距离2m;
,抛物线上的最高点到水面的距离2m;
(2)若水面上升1m后到达BC位置,如图,
当![]() 时,
时,![]() ,
,
解得![]() ,
,![]() ,
,
![]() .
.
故水面宽约为![]() .
.

练习册系列答案
相关题目