题目内容
【题目】如图，已知抛物线
与x轴交于A、B两点，其中点A的坐标为
，抛物线的顶点为P．
求b的值，并求出点P、B的坐标；
在x轴下方的抛物线上是否存在点M，使
≌
？如果存在，请直接写出点M的坐标；如果不存在，试说明理由．
【答案】
存在，
【解析】
（1）将点A的坐标代入抛物线的解析式可求得b的值，从而得到抛物线的解析式，然后利用配方法对抛物线的解析式进行变形可求得点P的坐标，接下来，令y=0得到关于x的方程可求得点B的横坐标；
（2）过点P作PC⊥x轴，垂足为C，连接AP、BP，作∠PAB的平分线，交PB与点N，交抛物线与点M，连接PM、BM，求得AB、AP、BP的长，然后可证明PN=PB，从而可求得点N的坐标，然后再求得AM的解析式，最后求得直线AM与抛物线的交点M的坐标即可.
抛物线
经过
，
，解得：
，
抛物线的表达式为
．
，
点P的坐标为
令
得：
，解得
或
，
的坐标为
．
存在，点
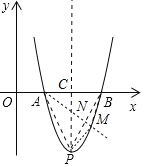
如图：过点P作
轴，垂足为C，连接AP、BP，作
的平分线，交PB与点N，交抛物线与点M，连接PM、BM．
，
，
，
，
，
，
是等边三角形，
，
．
，
，
．
在
和
中，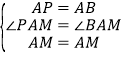
，
≌．
存在这样的点M，使得≌．
，，点N是PB的中点，
设直线AM的解析式为
，将点A和点N的坐标代入得：
，解得：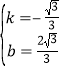
，
直线AM的解析式为
．
将代入抛物线的解析式得：
，解得：
或
舍去
，
当时，
，
点M的坐标为
练习册系列答案
相关题目
