题目内容
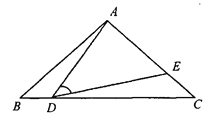
【题目】如图,在△ABC中,AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线段BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE.
(1)运动 秒时,AE=![]() DC(不必说明理由)
DC(不必说明理由)
(2)运动多少秒时,∠ADE=90°-![]() ∠BAC,并请说明理由;
∠BAC,并请说明理由;
【答案】(1)3;(2)运动![]() 秒时,∠ADE=90°
秒时,∠ADE=90°![]() ∠BAC.
∠BAC.
【解析】
(1)设运动的时间是t秒,则CD=12-2t,AE=9-2t,得出方程9-2t=![]() (12-2t),求出方程的解即可;(2)求出∠B=∠C=∠ADE,推出∠BAD=∠EDC,根据AAS证△ABD≌△DCE,推出DC=AB=9即可.
(12-2t),求出方程的解即可;(2)求出∠B=∠C=∠ADE,推出∠BAD=∠EDC,根据AAS证△ABD≌△DCE,推出DC=AB=9即可.
(1)设运动的时间是t秒,
则CD=122t,AE=92t,
92t=![]() (122t)
(122t)
t=3,
故答案为:3.
(2)设x秒后,∠ADE=90°![]() ∠BAC,
∠BAC,
∵∠B=∠C=90°![]() ∠BAC,
∠BAC,
∴∠B=∠C=∠ADE,
∵∠BAD+∠ADB+∠B=180°,∠EDC+∠ADE+∠ADB=180°,
∴∠BAD=∠EDC,
在△ABD和△DCE中,
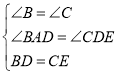
∴△ABD≌△DCE(AAS),
∴DC=AB=9,
∴BD=3,
∴x=![]() ,
,
即运动![]() 秒时,∠ADE=90°
秒时,∠ADE=90°![]() ∠BAC.
∠BAC.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目