Question

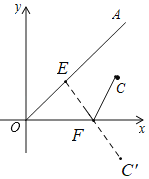
【题目】在平面直角坐标系中，射线OA是第一象限的角平分线，点C（11，5），E，F分别是射线OA和x轴正半轴的动点，那么FE+FC的最小值是_____．

Answer 1

【答案】8．

【解析】

作点C关于x轴的对称点C'，过点C作CF⊥OA于点E，交x轴于点F．FC＝FC'，FE+FC＝FE+FC'＝C'E，当C'E⊥OA时，C'E最小，即FE+FC的最小．

解：作点C关于x轴的对称点C'，过点C作CF⊥OA于点E，交x轴于点F．

则FC＝FC'，

FE+FC＝FE+FC'＝C'E，当C'E⊥OA时，C'E最小，即FE+FC的最小．

∵C（11，5），

∴C'（11，﹣5），

射线OA是第一象限的角平分线，

设直线EC'：y＝﹣x+b，

将C'（11，﹣5）代入，

﹣5＝﹣11+b，

解得b＝6，

∴直线EC'：y＝﹣x+6，

设E（m，m），

则m＝﹣m+6，

m＝3，

E（3，3），

∴EC'＝＝8

即FE+FC的最小值是8．

故答案为8．