题目内容
【题目】如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
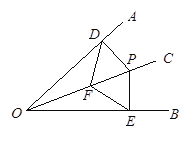
【答案】证明见解析.
【解析】
试题证明线段相等的方法一般是三角形的全等,找到包含两条线段的两个三角形△DPF和△EPF,然后找全等的条件,角平分线线上的点到两边的距离相等,所以PD=PE,因为PE⊥OB,PD⊥AO,所以∠PDO=
∠PEO=90°,所以∠DPF=90°-∠DOP,∠EPF=90°-∠EOP,即∠DPF=∠EPF,在△DPF和△EPF中, PD="PE," ∠DPF=∠EPF,PF=PF,所以△DPF≌△EPF,所以DF=EF.
试题解析:∵点P在∠AOB的角平分线OC上,PE⊥OB,PD⊥AO,
∴PD=PE,∠DOP=∠EOP,∠PDO=∠PEO=90°,
∴∠DPF=90°-∠DOP,∠EPF=90°-∠EOP,
∴∠DPF=∠EPF,
在△DPF和△EPF中,
PD="PE," ∠DPF=∠EPF,PF=PF,
∴△DPF≌△EPF(ASA),
∴DF=EF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】科技馆门票价格规定如下表:
购票张数 |
|
| 100张以上 |
每张票的价格 | 18元 | 15元 | 10元 |
风鸣学校七年级![]() 、
、![]() 两个科技班共103人去科技馆,其中
两个科技班共103人去科技馆,其中![]() 班有40多人不足50人
班有40多人不足50人![]() 经计算,如果两个班都以班为单位购票,则一共应付1686元.
经计算,如果两个班都以班为单位购票,则一共应付1686元.
![]() 如果两个班联合起来,作为一个团体购票,可以省______元
如果两个班联合起来,作为一个团体购票,可以省______元![]()
![]() 七年级
七年级![]() 班有多少学生?
班有多少学生?
![]() 如果七年级
如果七年级![]() 班单独组织去科技馆,作为组织者,你如何购票才最省钱?
班单独组织去科技馆,作为组织者,你如何购票才最省钱?