题目内容
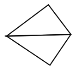
【题目】如图，在△ABC中，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G，若∠BAC=100°，则∠EAG=_____．
【答案】：20°
【解析】
由∠BAC=100°，可求得∠B+∠C的度数，又由AC的垂直平分线分别交AC、BC于点F、G，则可求得AE=BE，AG=CG，继而求得∠BAE+∠CAG的度数，则可求得答案．
∵∠BAC=100°，
∴∠B+∠C=180°∠BAC=80°，
∵AB的垂直平分线分别交AB、BC于点D. E，
∴AE=BE，AG=CG，
∴∠BAE=∠B，∠CAG=∠C，
∴∠BAE+∠CAG=∠B+∠C=80°，
∴∠EAG=∠BAC(∠BAE+∠CAG)=20°.
故答案为：20°.
练习册系列答案
相关题目
