题目内容
“惠民”经销店为某工厂代销一种工业原料(代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨;该经销店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨工业原料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)若在“薄利多销、让利于民”的原则下,当每吨原料售价为多少时,该店的月利润为9000元;
(3)每吨原料售价为多少时,该店的月利润最大,求出最大利润.
(1)60吨;(2)200元或220元;(3)210元,9075元.
解析试题分析:(1)因为每吨售价每下降10元时,月销售量就会增加7.5吨,可求出当每吨售价是240元时,此时的月销售量是多少吨;(2)设当售价定为每吨x元时,根据当每吨售价为260元时,月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元,当每吨售价每下降10元时,月销售量就会增加7.5吨,且该经销店计划月利润为9000元而且尽可能地扩大销售量,以9000元做为等量关系可列出方程求解;(3)求出月利润关于每吨原料售价的函数,即可得出答案.
试题解析:(1)当每吨的售价为240元时,月销售量= (吨).
(吨).
(2)设当每吨原料售价为x元时,该店的月利润为9000元.
由题意得: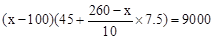 ,
,
整理得: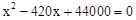 ,
,
解得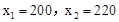 .
.
∴当每吨原料售价为200元或220元,该店的月利润为9000元.
(3)当每吨原料售价为x元时,
月利润=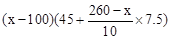 =
=
∵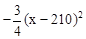 £0,当
£0,当 =210元时,月利润最大,为9075元.
=210元时,月利润最大,为9075元.
考点:1.一元二次方程的应用;2. 二次函数的应用.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案中秋节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.
九(1)班数学建模兴趣小组根据调查,整理出第x天( )的捕捞与销售的相关信息如下:
)的捕捞与销售的相关信息如下:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) |  |
| 捕捞量(kg) | 950-10x |
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x天的收入y(元)与x(元)之间的函数关系式;(当天收入=日销售额
 日捕捞成本)
日捕捞成本)(3)试说明(2)中的函数y随x的变化情况,并指出在第几天y取得最大值,最大值是多少?
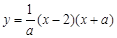
 与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.

 与
与 轴交于点
轴交于点 .
.
 (2,0),求平移后的抛物线解析式;
(2,0),求平移后的抛物线解析式;  (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推. (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.