题目内容
如图,已知抛物线 与
与 轴交于点
轴交于点 .
.
(1)平移该抛物线使其经过点 和点
和点 (2,0),求平移后的抛物线解析式;
(2,0),求平移后的抛物线解析式;
(2)求该抛物线的对称轴与(1)中平移后的抛物线对称轴之间的距离.
(1)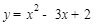 ;(2)两对称轴之间的距离为
;(2)两对称轴之间的距离为 .
.
解析试题分析:(1)由原抛物线求得点 的坐标,由点
的坐标,由点 和点
和点 坐标求得平移后的抛物线解析式;(2)求得原抛物线和平移后抛物线的对称轴,则可得到两对称轴间的距离.
坐标求得平移后的抛物线解析式;(2)求得原抛物线和平移后抛物线的对称轴,则可得到两对称轴间的距离.
试题解析:(1)设平移后的抛物线解析式为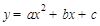 .由已知得
.由已知得 ,
,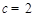 ,
,
∴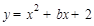 .
. 过点
过点
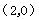 ,∴
,∴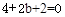 . ∴
. ∴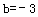 ,∴
,∴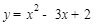 .
.
(2)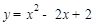 的对称轴为直线
的对称轴为直线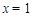 ,
,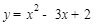 的对称轴为直线
的对称轴为直线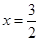 ,
,
∴两对称轴之间的距离为 .
.
【考点】1.二次函数解析式的求法;2.二次函数的图象.

练习册系列答案
相关题目

 的图象
的图象 ,将其向右平移两个单位后得到图象
,将其向右平移两个单位后得到图象 .
.
 轴相交于点
轴相交于点 、点
、点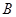 (点
(点 ,点
,点 位于
位于 轴负半轴上,且到
轴负半轴上,且到 所在直线的解析式.
所在直线的解析式. 与x轴交与点A(1,0)与点B, 且过点C(0,3),
与x轴交与点A(1,0)与点B, 且过点C(0,3),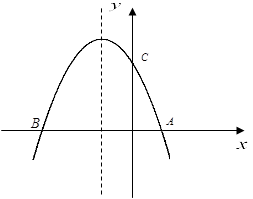

 时,S与t之间的函数关系式.
时,S与t之间的函数关系式. (a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程
(a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程 的两根.
的两根.
 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.