题目内容
【题目】完成下面的证明：
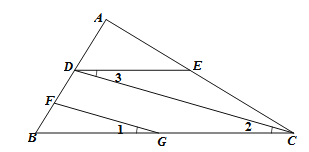
如图，FG//CD，∠1=∠3，∠B=50°，求∠BDE的度数．
解：∵FG//CD (已知)
∴∠2=_________（ ）
又∵∠1=∠3
∴∠3=∠_________（ ）
∴BC//__________（ ）
∴∠B+________=180°（ ）
又∵∠B=50°
∴∠BDE=130°．
【答案】∠1；两直线平行，同位角相等；∠2；等量代换；DE；内错角相等，两直线平行；∠BDE；两直线平行，同旁内角互补
【解析】
由两直线平行，同位角相等，得到∠2=∠1，再由等式的性质得到∠3=∠2，从而得到BC//DE，再由平行线的性质得到∠B+∠BDE=180°，从而得到结论．
解：∵FG//CD(已知)
∴∠2=∠1（两直线平行，同位角相等）
又∵∠1=∠3，
∴∠3=∠2（等量代换）
∴BC//DE（内错角相等，两直线平行）
∴∠B+∠BDE=180°（两直线平行，同旁内角互补）
又∵∠B=50°
∴∠BDE=130°．
故答案为：∠1；两直线平行，同位角相等；∠2；等量代换；DE；内错角相等，两直线平行；∠BDE；两直线平行，同旁内角互补．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
