Question

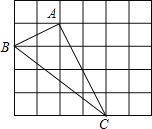
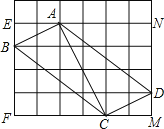
【题目】如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：

(1)画线段AD∥BC且使AD=BC，连接CD；

(2)线段AC的长为___，CD的长为___，AD的长为___.

(3)试判断△ACD的形状，并求四边形ABCD的面积.

Answer 1

【答案】（1）画图见解析；（2）2，，5；（3）直角，10.

【解析】

（1）根据题目要求结合网格画图即可；

（2）把线段AC、CD、AD放在一个直角三角形中利用勾股定理计算即可；

（3）根据勾股定理的逆定理即可判断△ACD的形状，用矩形EFMN的面积-四周4个三角形的面积=四边形ABCD的面积．

（1）如图所示：

（2）AC=；

CD=；

AD==5；

（3）∵（2）2+（）2=52，

∴△ACD是直角三角形，

S四边形ABCD=4×6-×2×1-×4×3-×2×1-×3×4=10．