题目内容
【题目】如图，△ABC中，AB=AC，AD是△ABC外角的平分线，已知∠BAC=∠ACD．
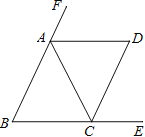
（1）求证：△ABC≌△CDA；
（2）若∠B=60°，求证：四边形ABCD是菱形．
【答案】(1)证明见解析；（2）证明见解析.
【解析】试题分析：（1）求出∠B=∠ACB，根据三角形外角性质求出∠FAC=2∠ACB=2∠DAC，推出∠DAC=∠ACB，根据ASA证明△ABC和△CDA全等；
（2）推出AD∥BC，AB∥CD，得出平行四边形ABCD，根据∠B=60°，AB=AC，得出等边△ABC，推出AB=BC即可．
证明：（1）∵AB=AC，
∴∠B=∠ACB，
∵∠FAC=∠B+∠ACB=2∠ACB，
∵AD平分∠FAC，
∴∠FAC=2∠CAD，
∴∠CAD=∠ACB，
∵在△ABC和△CDA中
，
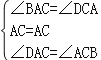∴△ABC≌△CDA（ASA）；
（2）∵∠FAC=2∠ACB，∠FAC=2∠DAC，
∴∠DAC=∠ACB，
∴AD∥BC，
∵∠BAC=∠ACD，
∴AB∥CD，
∴四边形ABCD是平行四边形，
∵∠B=60°，AB=AC，
∴△ABC是等边三角形，
∴AB=BC，
∴平行四边形ABCD是菱形．
练习册系列答案
相关题目
【题目】（10分）每年的6月5日为世界环保日，为提倡低碳环保，某公司决定购买10台节省能源的新机器，现有甲、乙两种型号的新机器可选，其中每台的价格、工作量如下表．
甲型机器 | 乙型机器 | |
价格（万元/台） | a | b |
产量（吨/月） | 240 | 180 |
经调查：购买一台甲型机器比购买一台乙型机器多2万元，购买2台甲型机器比购买3台乙型机器少6万元．
（1）求a、b的值；
（2）若该公司购买新机器的资金不能超过110万元，请问该公司有几种购买方案？
（3）在（2）的条件下，若公司要求每月的产量不低于2040吨，请你为该公司设计一种最省钱的购买方案．
