题目内容
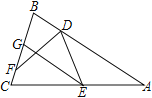
【题目】感知:如图①,△ABC是等腰直角三角形,∠ACB=90°,正方形CDEF的顶点D,F分别在边AC,BC上,易证:AD=BF(不需要证明);
(1)探究:将图①的正方形CDEF绕点C顺时针旋转α(0°<α<90°),连接AD,BF,其他条件不变,如图②,求证:AD=BF;
(2)应用:若α=45°,CD= ![]() ,BE=1,如图③,则BF= .
,BE=1,如图③,则BF= .
【答案】
(1)
证明:如图②,
∵四边形CDEF为正方形,
∴CD=CF,
由旋转得:∠ACD=∠BCF,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,
∴△ADC≌△BFC,
∴AD=BF;
(2)![]()
【解析】应用:如图③,∵四边形CDEF为正方形,
∴∠EDC=90°,ED=DC,
∵DC= ![]() ,
,
∴EC= ![]() =
= ![]() =2,
=2,
∴BC=BE+EC=1+2=3,
∴AC=BC=3,
过D作DG⊥AC于G,
∵α=45°,
即∠ACD=45°,
∴△DCG是等腰直角三角形,
∴DG=CG=1,
∴AG=BC﹣CG=3﹣1=2,
由勾股定理得:AD= ![]() =
= ![]() =
= ![]() ,
,
同理得:△ADC≌△BFC,
∴BF=AD= ![]() .
.
【考点精析】通过灵活运用等腰直角三角形和勾股定理的概念,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目