题目内容
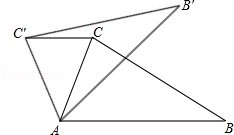
（2013年四川攀枝花3分）如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=【 】
| A．30° | B．35° | C．40° | D．50° |
A。
∵△ABC绕点A旋转到△AB′C′的位置，∴AC=AC′，∠BAC=∠B′AC′。
∵CC′∥AB，∠CAB=75°，∴∠ACC′=∠CAB=75°。∴∠CAC′=180°﹣2∠ACC′=180°﹣2×75°=30°。
∵∠BAB′=∠BAC﹣∠B′AC，∠CAC′=∠B′AC′﹣∠B′AC，
∴∠BAB′=∠CAC′=30°。故选A。
∵CC′∥AB，∠CAB=75°，∴∠ACC′=∠CAB=75°。∴∠CAC′=180°﹣2∠ACC′=180°﹣2×75°=30°。
∵∠BAB′=∠BAC﹣∠B′AC，∠CAC′=∠B′AC′﹣∠B′AC，
∴∠BAB′=∠CAC′=30°。故选A。
练习册系列答案
相关题目
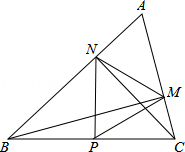
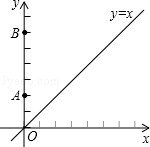
．试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB=
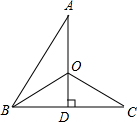
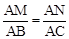；③△PMN为等边三角形；④当∠ABC=45°时，BN=
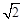PC．其中正确的个数是
