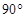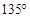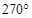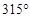题目内容
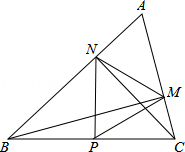
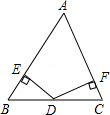
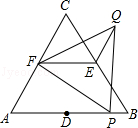
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②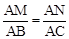 ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=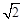 PC.其中正确的个数是
PC.其中正确的个数是
A.1个 B.2个 C.3个 D.4个
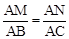 ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=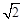 PC.其中正确的个数是
PC.其中正确的个数是
A.1个 B.2个 C.3个 D.4个
D
试题分析:①∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
∴PM=
 BC,PN=
BC,PN= BC。∴PM=PN。正确。
BC。∴PM=PN。正确。②在△ABM与△ACN中,∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,∴
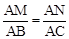 。正确。
。正确。③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,∴∠ABM=∠ACN=30°。
在△ABC中,∠BCN+∠CBM═180°﹣60°﹣30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,∴PM=PN=PB=PC。
∴∠BPN=2∠BCN,∠CPM=2∠CBM。∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°。
∴∠MPN=60°。∴△PMN是等边三角形。正确。
④当∠ABC=45°时,∵CN⊥AB于点N,∴∠BNC=90°,∠BCN=45°。∴BN=CN。
∵P为BC边的中点,∴PN⊥BC,△BPN为等腰直角三角形。
∴BN=
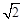 PB=
PB=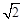 PC。正确。
PC。正确。综上所述,正确的结论个数是4个。故选D。

练习册系列答案
相关题目
 ,求AD的长.
,求AD的长.
 中,
中,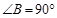 ,若按图中虚线剪去
,若按图中虚线剪去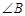 ,则
,则 等于( )
等于( )