题目内容
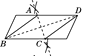
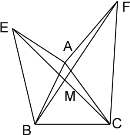
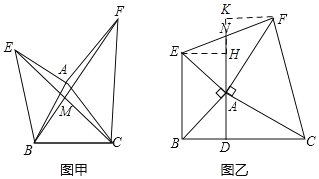
【题目】如图甲所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC. BF与CE相交于点M
(1)求证:①△ACE≌△AFB;②EC⊥BF.
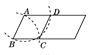
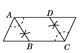
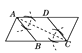
(2)如图乙连接EF,画出△ABC边BC上的高线AD,延长DA交EF于点N,其他条件不变,下列四个结论:①∠EAN=∠ABC;
②△AEN≌△BAD;③![]() ;④EN=FN。
;④EN=FN。
正确的结论是____________(把正确结论的序号全部填上)

【答案】(1)见解析(2)①③④.
【解析】
(1)先根据AE⊥AB,AF⊥AC,AE=AB,AF=AC判定△ACE≌△AFB(SAS);再根据全等三角形的性质得出∠ACM=∠AFM,根据Rt△ACF中,∠AFM+∠MFC+∠ACF=90°,可得∠ACM+∠MFC+∠ACF=90°,即△MCF是直角三角形,进而得出结论;
(2)先作EH⊥AN,交AN于点H,FK⊥AN,交AN延长线于点K,构造三对全等三角形:△AEH≌△BAD,△AFK≌△ACD,△FKN≌△EHN,根据全等三角形的面积相等,即可得出S△ABD=S△EAH,S△FKA=S△ADC,S△ENH=S△FNK,根据S△ABC=S△ABD+S△ADC=S△AEH+S△AFK=(S△EAN-S△ENH)+(S△FNA+S△FNK)=S△EAN+S△FNA=S△AEF,即可得出结论③;最后根据△FKN≌△EHN,得出FN=EN即可.
(1)证明:①∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAF=∠EAC,
在△ACE和△AFB中,
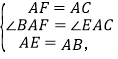
∴△ACE≌△AFB(SAS);
②∵△ACE≌△AFB,
∴∠ACM=∠AFM,
∵Rt△ACF中,∠AFM+∠MFC+∠ACF=90°,
∴∠ACM+∠MFC+∠ACF=90°,
即△MCF是直角三角形,
∴∠CMF=90°,即CE⊥BF;
(2)∵∠BAE=90°,AD⊥BD,
∴∠EAN+∠BAD=90°=∠ABC+∠BAD,
∴∠EAN=∠ABC,故①正确;
∵∠AEN与∠BAD不一定相等,
∴△AEN与△BAD不一定全等,故②错误;
作EH⊥AN,交AN于点H,FK⊥AN,交AN延长线于点K,
∴∠AEH+∠EAH=90°,
∵∠EAB=90°,
∴∠EAH+∠BAD=90°,
∴∠AEH=∠BAD,
在△AEH和△BAD中,

∴△AEH≌△BAD(AAS),
∴EH=AD,
同理可得:△AFK≌△ACD,
∴FK=AD,
∴FK=EH,
在△FKN和△EHN中,
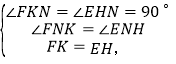
∴△FKN≌△EHN(AAS),
∴![]()
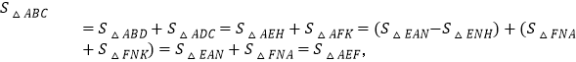 即
即![]() 故③正确;
故③正确;
∵△FKN≌△EHN,
∴FN=EN,故④正确.
故答案为:①③④.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案