��Ŀ����
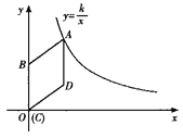
����Ŀ����ͼ����֪��ABC�У�AB=AC=12cm����![]() ��BC=10cm����DΪAB���е㣮�����P���߶�BC����2cm/s���ٶ��ɵ�B��C���˶���ͬʱ����Q���߶�AC���ɵ�A��C����4cm/s���ٶ��˶���
��BC=10cm����DΪAB���е㣮�����P���߶�BC����2cm/s���ٶ��ɵ�B��C���˶���ͬʱ����Q���߶�AC���ɵ�A��C����4cm/s���ٶ��˶���
��1������P��Q����ֱ��B��A����ͬʱ����������2���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������P��Q����ֱ��B��A����ͬʱ��������CPQ���ܳ�Ϊ18cm���ʣ����������CPQ�ǵ��������Σ�

���𰸡���1����BPD���CQP��ȫ�ȣ����ɼ���������2������1���![]() ���
���![]() ��ʱ����CPQ�ǵ���������.
��ʱ����CPQ�ǵ���������.
��������
��1������2���PB=4m��PC=6m��CQ=4m������֪�ɵ�BD=PC��BP=CQ����ABC=��ACB������SAS��֤�á�BPD�ա�CQP��
��2�������Q���˶�ʱ��Ϊts��CPQ�ǵ��������Σ����֪PB=2tcm��PC=8-3tcm��CQ=xtcm���ݣ�1��ͬ���ɵõ�BD=PC��BP=CQ��BD=CQ��BP=PCʱ��CPQΪ���������Σ��Ӷ����t��ֵ��
��1����BPD���CQP��ȫ�ȣ��������£�
��P��Q����ֱ��B��A����ͬʱ�����˶�2��ʱ��BP=2��2=4cm��AQ=4��2=8cm��
��CP=BC-BP=10-4=6cm��CQ=AC-AQ=12-8=4cm ��
��D��AB���е㣬��BD=![]() AB=
AB=![]() ��12=6cm��
��12=6cm��
��BP=CQ��BD=CP���֡ߡ�ABC�У�AB=AC�����B=��C ��
�ڡ�BPD�͡�CQP��
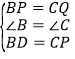
���BPD�ա�CQP��SAS��
��2���赱P��Q����ͬʱ�����˶�t��ʱ����BP=2t��AQ=4t,
��t��ȡֵ��ΧΪ0��t��3
��CP=10-2t��CQ=12-4t ,
�ߡ�CPQ���ܳ�Ϊ18cm��
��PQ=18-��10-2t��-�� 12-4t��=6t-4
Ҫʹ��CPQ�ǵ��������Σ���ɷ�Ϊ����������ۣ�
�ٵ�CP=CQʱ������10-2t=12-4t����ã�t=1
�ڵ�PQ=PCʱ������6t-4=10-2t����ã�t=![]() ��
��
�۵�QP=QCʱ������6t-4=12-4t����ã�t=![]() ��
��
�������������t��ȡֵ��Χ��
��������������1���![]() ���
���![]() ��ʱ����CPQ�ǵ���������.
��ʱ����CPQ�ǵ���������.