��Ŀ����
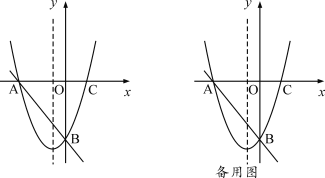
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�A�͵�B.������
��ֱ��ڵ�A�͵�B.������![]() ����A,B���㣬�ҶԳ���Ϊֱ��
����A,B���㣬�ҶԳ���Ϊֱ��![]() ����������
����������![]() �����һ����Ϊ��C.
�����һ����Ϊ��C.
��1���������ߵĺ�������ʽ��
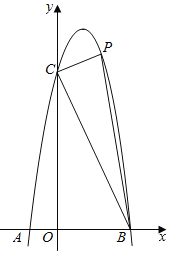
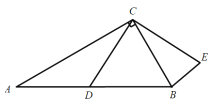
��2�����E����������һ���㣬�ҵ�E��ֱ��AB�·�.����ABE��������ʱ�����E�����꣬����ABE��������ֵS��
���������Ƿ���������M,ʹ��ABM����������е����ֵS,�����ڣ�������������ĵ�M�����ꣻ�������ڣ�˵�����ɣ�
��3������FΪ�߶�OB��һ���㣬ֱ��д��![]() ����Сֵ.
����Сֵ.
���𰸡���1��![]() ����2��E(-2,-4��,4�������ڣ�
����2��E(-2,-4��,4�������ڣ�![]() ����3��
����3��![]()
��������
��1�����AB�������꣬���ô���ϵ����������⣻
��2�����E������Ϊ![]() ������ABE��������ʱ����E�����������Ҿ�AB��Զ����ʱE����ֱ����ABƽ�У�����������ֻ��һ������.���E����ֱ��Ϊl��y=-x+b������κ������������飬����ֻ��һ�����㣬��
������ABE��������ʱ����E�����������Ҿ�AB��Զ����ʱE����ֱ����ABƽ�У�����������ֻ��һ������.���E����ֱ��Ϊl��y=-x+b������κ������������飬����ֻ��һ�����㣬��![]() �����b�����������E���ꣻ
�����b�����������E���ꣻ
��������ֱ��AB�Ϸ�������������M,ʹ��ABM����������е����ֵS����ʱ��M����ֱ��![]() ��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ����ֱ��
��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ����ֱ��![]() ����ʽ������κ������������飬������⣻
����ʽ������κ������������飬������⣻
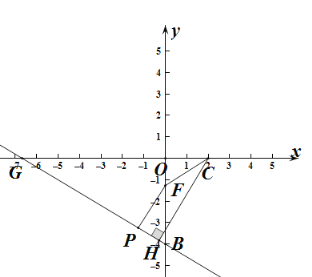
��3����ͼ����![]() ��x���ڵ�G����FP��BG����P���õ�
��x���ڵ�G����FP��BG����P���õ�![]() �����Ե�C��F��P��ͬһֱ����ʱ��
�����Ե�C��F��P��ͬһֱ����ʱ�� ![]() ����Сֵ����CH��GB��H�����CH���ɣ�
����Сֵ����CH��GB��H�����CH���ɣ�
�⣺��1����![]() �зֱ���x=0��y=0���ɵõ�A(-4,0)��B(0,-4)��
�зֱ���x=0��y=0���ɵõ�A(-4,0)��B(0,-4)��
����A,B���꼰�Գ���Ϊֱ��![]() ���ɵ÷�����
���ɵ÷�����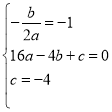
�ⷽ����ɵ�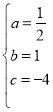
�������ߵĺ�������ʽΪ![]()
��2�������E������Ϊ![]() ������ABE��������ʱ��
������ABE��������ʱ��
��E�����������Ҿ�AB��Զ����ʱE����ֱ����ABƽ�У�����������ֻ��һ������.���E����ֱ��Ϊl��y=-x+b.
�����÷���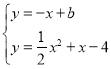 ����ȥy
����ȥy
��![]() ��������
��������![]() ��
��
��֮��![]() ��ֱ��l�Ľ���ʽΪy=-x-6,
��ֱ��l�Ľ���ʽΪy=-x-6,
��������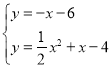 �����
�����![]() ��
��
���E(-2,-4����
��E��y���ƽ���߿������ABE��������ֵΪ4.
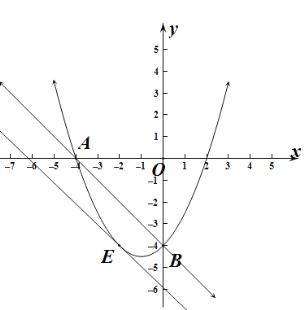
����������ֱ��AB�Ϸ�������������M,ʹ��ABM����������е����ֵS����ʱ��M����ֱ��![]() ��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ���ֱ��
��ֱ��ABƽ��,����ֱ��l��ֱ��AB������ȣ���ֱ��![]() ��ֱ��l����ƽ��4����λ��
��ֱ��l����ƽ��4����λ��
�����ʽ![]() Ϊy=-x-2,����κ�������������ɵ�
Ϊy=-x-2,����κ�������������ɵ�
������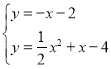 ��֮��
��֮��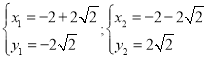
����������㣬![]()
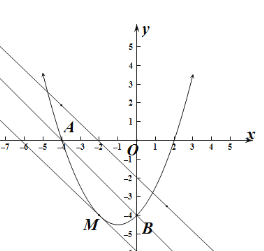
��3����ͼ����![]() ��x���ڵ�G����FP��BG��P��
��x���ڵ�G����FP��BG��P��
��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��![]() ,
,
��![]() ,
,
�൱C��F��P��ͬһֱ����ʱ�� ![]() ����Сֵ��
����Сֵ��
��CH��GB��H��
��![]() ����
���� ![]()
��![]() ,
,![]() ,
,
��A(-4,0)�������߶Գ���Ϊֱ��![]() ��
��
���C������2,0����
��![]() ,
,
�� ��![]() ��
�У�![]() ,
,
��![]() ����СֵΪ
����СֵΪ![]() ��
��