题目内容
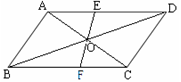
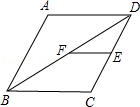
如图,正方形ABCD中,O是对角线AC、BD的交点,过点O作OE⊥OF,分别交AB、BC于E、F.
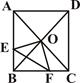
(1)求证:△OEF是等腰直角三角形.
(2)若AE=4,CF=3,求EF的长.

(1)求证:△OEF是等腰直角三角形.
(2)若AE=4,CF=3,求EF的长.
(1)根据正方形的性质可得∠ABO=∠ACF=45°,OB=OC,∠BOC=90°,再结合DE⊥OF可得∠EOB=∠FOC,即可证得△BEO≌△CFO,从而得到结论;(2)5
试题分析:(1)根据正方形的性质可得∠ABO=∠ACF=45°,OB=OC,∠BOC=90°,再结合DE⊥OF可得∠EOB=∠FOC,即可证得△BEO≌△CFO,从而得到结论;
(2)由△BEO≌△CFO可得BE=CF,根据正方形的性质可得AB=BF,再根据勾股定理求解即可.
(1)∵四边形ABCD为正方形
∴∠ABO=∠ACF=45°,OB=OC,∠BOC=90°
又∵DE⊥OF
∴∠EOF=90°
∴∠EOB=∠FOC
∴△BEO≌△CFO
∴OE=OF
又∠EOF=90°
∴△DEF是等腰直角三角形;
(2)∵△BEO≌△CFO(已证)
∴BE=CF
又∵四边形ABCD是正方形,
∴AB=BF
在Rt△BEF中,EF2=BE2+BF2 =CF2+AE2=32+42=52
∴EF=5
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中半径常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
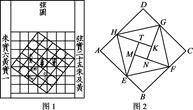
 是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )
是位似中心,F、G、H、M、N分别是OA、OB、OC、OD、OE的中点,则五边形ABCDE与五边形FGHMN的面积比是( )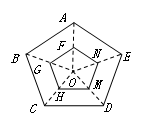
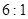 B.
B.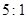 C.
C.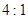 D.
D.
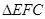 的面积为 .
的面积为 .