题目内容
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=﹣ ![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
【答案】
(1)
解:∵正方形OABC的边长为2,
∴点B、C的坐标分别为(2,2),(0,2),
∴ 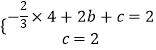 ,
,
解得 ![]() ,
,
∴二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:令y=0,则﹣ ![]() x2+
x2+ ![]() x+2=0,
x+2=0,
整理得,x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
∴二次函数与x轴的交点坐标为(﹣1,0)、(3,0),
∴当y>0时,x的取值范围是﹣1<x<3
【解析】(1)根据正方形的性质得出点B、C的坐标,然后利用待定系数法求函数解析式解答;(2)令y=0求出二次函数图象与x轴的交点坐标,再根据y>0,二次函数图象在x轴的上方写出x的取值范围即可.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】初三(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如表:
打字数/个 | 50 | 51 | 59 | 62 | 64 | 66 | 69 |
人数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个字)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次打字成绩的众数是个,平均数是个.