题目内容
【题目】如图，是二次函数y=ax2+bx+c的图象，对下列结论①ab＞0，②abc＞0，③ 
＜1，其中错误的个数是（ ） 
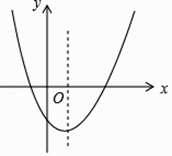
A.3
B.2
C.1
D.0
【答案】C
【解析】解：∵抛物线的开口向上， ∴a＞0，
∵对称轴在y轴的右侧，
∴b＜0，
∴ab＜0，故①错误；
∵抛物线和y轴的负半轴相交，
∴c＜0，
∴abc＞0，故②正确；
∵抛物线与x轴有两个交点，
∴b2﹣4ac＞0，
∴ 
＜1，故③正确；
故选C．
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）即可以解答此题．
练习册系列答案
相关题目
【题目】我市雷雷服饰有限公司生产了一款夏季服装，通过实体商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天的跟踪调查，其中实体商店的日销售量y1（百件）与时间t（t为整数，单位：天）的部分对应值如下表所示，网上商店的日销售量y2（百件）与时间t（t为整数，单位：天）的部分对应值如图所示．
时间t（天） | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量 | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
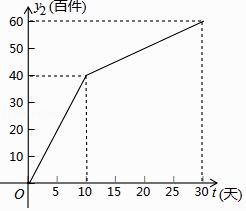
（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映y1与t的变化规律，并求出y1与t的函数关系式及自变量t的取值范围；
（2）求y2与t的函数关系式，并写出自变量t的取值范围；
（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为y（百件），求y与t的函数关系式；当t为何值时，日销售总量y达到最大，并求出此时的最大值．
