Question

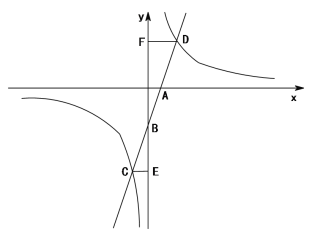
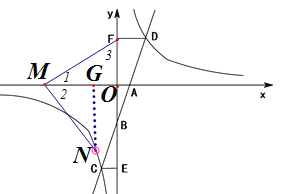
【题目】如图，一次函数y=k1x-3(k1＞0)的图象与x轴、y轴分别交于A，B两点，

与反比例函数y=(k2＞0)的图象交于C,D两点，作CE⊥y轴，垂足为点E，作DF⊥y轴，垂足为点F，已知CE=1．

(1) ①直接写出点C的坐标 (用k1来表示)

②k2﹣k1=　 　；

(2) 若B为AC的中点，求反比例函数的表达式；

(3) 在(2)的条件下，设点M是x轴负半轴上一点，将线段MF绕点M按顺时针或逆时针方向旋转90°得到线段MN，当点M滑动时，点N能否在反比例函数的图象上？如果能，求出点N的坐标；如果不能，请说明理由．

Answer 1

【答案】(1)①C ； ②3；(2) ；(3)能，N.

【解析】分析:（1）①由CE=1，可得点C横坐标-1，代入y=k1x-3，即可求出点C的纵坐标；②）联立y=k1x-3和y=，然后把x=-1代入整理即可；

（2）先证明△CBE≌△ABO,可得OB=BE.求出 y=k1x-3于y轴的交点B的坐标(-1,-3)，可得C点的坐标(-1,-6),用待定系数法即可求出反比例函数解析式；

（3）分MN绕点M顺时针旋转90°和MN绕点M逆时针旋转90°两种情况讨论解答即可.

详解:（1）①∵CE=1，

∴点C横坐标-1，

当x=-1时，

y=k1x-3=- k1-3，

∴C（-1，- k1-3）；

②由题意得，

k1x-3=，

把x=-1代入得，

- k1-3=-k2，

∴k2﹣k1=3;

（2）∵B为AC的中点，

∴AB=BC.

在△CBE和△ABO中，

∵∠CBE=∠ABO,

AB=BC

∠CEB=∠AOB=90°,

∴△CBE≌△ABO,

∴OB=BE.

把x=0代入y=k1x-3得，

y=-3,

∴B(-1,-3),

∴C(-1,-6),

把C(-1,-6)代入y=得，

k2=6,

∴.

（3）如图，当MN绕点M顺时针旋转90°时，点N在反比例函数图像上，作NG⊥x轴于点G.

把C(-1,-6)代入y=k1x-3得，

-k1-3=-6,

∴k1=3,

∴y=3x-3

解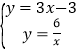 得，

，，

∴D（2,3），

∴OF=3.

∵∠1+∠2=90°,

∠1+∠3=90°,

∴∠2=∠3.

在△MOF和△NGM中，

∵∠2=∠3,

∠MGN=∠MOF,

MN=MF,

∴△MOF≌△NGM,

∴MG=OF=3.

设M（a,0）(a<0),则OG=-a-3,NG=OM=-a ,

∴N(a+3,a),

把N(a+3,a)代入得，

∴a(a+3)=6,

∴,（舍去），

∴a+3=+3=,

∴N.

当MN绕点M逆时针旋转90°时，点N在第二象限，此时点N不能落在反比例函数图像上.