题目内容
【题目】如图,点P(![]() +1,
+1, ![]() ﹣1)在双曲线y=kx-1(x>0)上.
﹣1)在双曲线y=kx-1(x>0)上.
(1)求k的值;
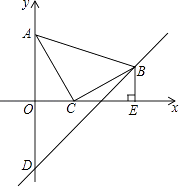
(2)若正方形ABCD的顶点C,D在双曲线y=kx-1(x>0)上,顶点A,B分别在x轴和y轴的正半轴上,求点C的坐标.
【答案】(1)k=2;(2) C的坐标为:(1,2).
【解析】分析:(1)将点P的坐标代入双曲线解析式中解答即可;(2)过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,易证得△CFB≌△BOA≌△AED,易得C(b,a+b),D(a+b,a),继而求得a的值,则可求得点C的坐标;
本题解析:
(1)点P(![]() +1,
+1, ![]() 1)在双曲线y=
1)在双曲线y=![]() (x>0)上,将x=
(x>0)上,将x=![]() +1,y=
+1,y=![]() 1代入解析式可得:k=2;
1代入解析式可得:k=2;
(2)过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,

∵四边形ABCD是正方形,∴AB=AD=BC,∠CBA=90°,∴∠FBC+∠OBA=90°,
∵∠CFB=∠BOA=90°,∴∠FCB+∠FBC=90°,∴∠FBC=∠OAB,
在△CFB和△AOB中,
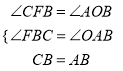 ,∴△CFB≌△AOB(AAS),
,∴△CFB≌△AOB(AAS),
同理可得:△BOA≌△AED≌△CFB,∴CF=OB=AE=b,BF=OA=DE=a,
设A(a,0),B(0,b),则D(a+b,a)C(b,a+b),可得:b(a+b)=2,a(a+b)=2,
解得:a=b=1.
所以点C的坐标为:(1,2).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目