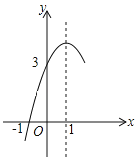题目内容
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )

A. 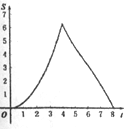 B.
B. 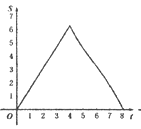
C. 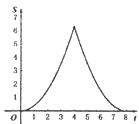 D.
D. 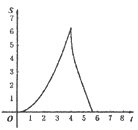
【答案】C
【解析】∵Rt△ABC中,∠A=90°,AB=AC=4,点E以每秒1个单位的速度从点C出发,
∴当0≤t≤4时,扇形面积S=![]() ,
,
∴前半段函数图象为开口向上的抛物线的一部分,故B选项错误;
当4<t≤8时,随着t的增大,扇形的半径增大,而扇形的圆心角减小,
∴后半段函数图象不是抛物线,故C选项错误;
∵当t=8时,点E、D重合,
∴扇形的面积为0,故D选项错误;
故选A.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目